Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shelah, Saharon
1975.
A compactness theorem for singular cardinals, free algebras, Whitehead problem and tranversals.
Israel Journal of Mathematics,
Vol. 21,
Issue. 4,
p.
319.
Dougherty, Daniel J
1987.
Decomposition of infinite matrices.
Journal of Combinatorial Theory, Series A,
Vol. 45,
Issue. 2,
p.
277.
Shelah, Saharon
1987.
Classification Theory.
Vol. 1292,
Issue. ,
p.
264.


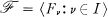 is a 1-1 map
is a 1-1 map