Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:43:01.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Sublattices and Initial Segments of the Degrees of Unsolvability

Published online by Cambridge University Press:  20 November 2018

S. K. Thomason
S. K. Thomason*
Affiliation:
University of California, Berkeley, California; Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall prove that every finite lattice is isomorphic to a sublattice of the degrees of unsolvability, and that every one of a certain class of finite lattices is isomorphic to an initial segment of degrees.

Acknowledgment. I am grateful to Ralph McKenzie for his assistance in matters of lattice theory.

1. Representation of lattices. The equivalence lattice 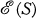of the set S consists of all equivalence relations on S, ordered by setting θ ≦ θ’ if for all a and b in S, a θ b ⇒ a θ’ b. The least upper bound and greatest lower bound in 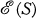are given by the ⋃ and ⋂ operations:

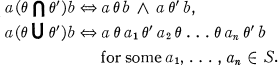
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 569 - 581
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bjarni, Jönsson, On the representations of lattices, Math. Scand. 1 (1953), 193–206.Google Scholar
2. Lachlan, A. H., Distributive initial segments of the degrees of unsolvability, Z. Math. Logik Grundlagen Math. 44 (1968), 457–472.Google Scholar
3. Manuel, Lerman, Some non-distributive lattices as initial segments of the degrees of unsolvability, J. Symbolic Logic 34 (1969), 85–98.Google Scholar
4. Sacks, Gerald E., Degrees of unsolvability (Princeton Univ. Press, Princeton, N. J., 1963).Google Scholar
5. Thomason, S. K., On initial segments of hyperdegrees, J. Symbolic Logic (to appear).Google Scholar
6. Thomason, S. K., A proof of Whitman's representation theorem for finite lattices, Proc. Amer. Math. Soc. (to appear).Google Scholar
7. Whitman, Philip M., Lattices, equivalence relations, and subgroups. Bull. Amer. Math. Soc. 52 (1946), 507–522.Google Scholar