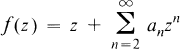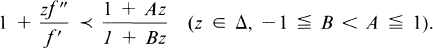Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sheil-Small, T.
and
Silvia, E. M.
1981.
Neighborhoods of analytic functions.
Journal d'Analyse Mathématique,
Vol. 52,
Issue. 1,
p.
210.
Shanmugam, T N
1986.
On a subclass of Bazilevic functions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 95,
Issue. 2,
Jahangiri, M
Silverman, H
and
Silvia, E.M
1990.
Inclusion relations between classes of functions defined by subordination.
Journal of Mathematical Analysis and Applications,
Vol. 151,
Issue. 2,
p.
318.
Silverman, Herb
1991.
A Survey with Open Problems on Univalent Functions Whose Coefficients are Negative.
Rocky Mountain Journal of Mathematics,
Vol. 21,
Issue. 3,
Ahuja, O.P.
1993.
On the generalised Ruscheweyh class of analytic functions of complex order.
Bulletin of the Australian Mathematical Society,
Vol. 47,
Issue. 2,
p.
247.
Gangadharan, A.
Ravichandran, V.
and
Shanmugam, T.N.
1997.
Radii of Convexity and Strong Starlikeness for Some Classes of Analytic Functions.
Journal of Mathematical Analysis and Applications,
Vol. 211,
Issue. 1,
p.
301.
Cho, Nak Eun
Kim, Yong Chan
and
Srivastava, H.M.
1999.
Argument Estimates for a Certain Class of Analytic Functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 38,
Issue. 3,
p.
277.
Cho, Nak Eun
2003.
The Noor integral operator and strongly close-to-convex functions.
Journal of Mathematical Analysis and Applications,
Vol. 283,
Issue. 1,
p.
202.
Cho, N.E.
and
Srivastava, H.M.
2003.
Argument estimates of certain analytic functions defined by a class of multiplier transformations.
Mathematical and Computer Modelling,
Vol. 37,
Issue. 1-2,
p.
39.
Cho, Nak Eun
Kwon, Oh Sang
and
Srivastava, H.M.
2004.
Inclusion and argument properties for certain subclasses of meromorphic functions associated with a family of multiplier transformations.
Journal of Mathematical Analysis and Applications,
Vol. 300,
Issue. 2,
p.
505.
Cho, Nak Eun
Kwon, Oh Sang
and
Srivastava, H.M.
2004.
Inclusion relationships and argument properties for certain subclasses of multivalent functions associated with a family of linear operators.
Journal of Mathematical Analysis and Applications,
Vol. 292,
Issue. 2,
p.
470.
Wang, Zhi-Gang
Gao, Chun-Yi
and
Yuan, Shao-Mou
2006.
On certain subclasses of close-to-convex and quasi-convex functions with respect to k-symmetric points.
Journal of Mathematical Analysis and Applications,
Vol. 322,
Issue. 1,
p.
97.
Kim, Yong Chan
and
Srivastava, H.M.
2006.
The Hardy space for a certain subclass of Bazilevič functions.
Applied Mathematics and Computation,
Vol. 183,
Issue. 2,
p.
1201.
Huang, Ya-Yuan
and
Liu, Ming-Sheng
2008.
Properties of certain subclasses of multivalent analytic functions involving the Dziok–Srivastava operator.
Applied Mathematics and Computation,
Vol. 204,
Issue. 1,
p.
137.
Aouf, M.K.
2008.
Argument estimates of certain meromorphically multivalent functions associated with generalized hypergeometric function.
Applied Mathematics and Computation,
Vol. 206,
Issue. 2,
p.
772.
Deni̇z, Erhan
and
Orhan, Halit
2010.
Some properties of certain subclasses of analytic functions with negative coefficients by using generalized ruscheweyh derivative operator.
Czechoslovak Mathematical Journal,
Vol. 60,
Issue. 3,
p.
699.
Aouf, M. K.
and
Seoudy, T. M.
2011.
Classes of analytic functions related to the Dziok–Srivastava operator.
Integral Transforms and Special Functions,
Vol. 22,
Issue. 6,
p.
423.
Shi, Lei
Yi, Jing-Ping
and
Wang, Zhi-Gang
2013.
On certain subclass of meromorphic close-to-convex functions.
Applied Mathematics and Computation,
Vol. 219,
Issue. 20,
p.
10143.
Kwon, Ohsang
and
Sim, Youngjae
2013.
A CERTAIN SUBCLASS OF JANOWSKI TYPE FUNCTIONS ASSOCIATED WITH κ-SYMMETRIC POINTS.
Communications of the Korean Mathematical Society,
Vol. 28,
Issue. 1,
p.
143.
Curt, Paula
2014.
JANOWSKI STARLIKENESS IN SEVERAL COMPLEX VARIABLES AND COMPLEX HILBERT SPACES.
Taiwanese Journal of Mathematics,
Vol. 18,
Issue. 4,