Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:49:02.539Z Has data issue: false hasContentIssue false
  • English
  • Français

The Structure of the Algebra of Hankel Transforms and the Algebra of Hankel-Stieltjes Transforms

Published online by Cambridge University Press:  20 November 2018

Alan Schwartz
Alan Schwartz*
Affiliation:
University of Missouri, Saint Louis, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

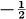Let M be the space of all bounded regular complex-valued Borel measures defined on I = [0, ∞). M is a Banach space with ‖μ‖ = ∫d|μ|(x) (μ ∈ M). (Integrals in this paper extend over all of I unless otherwise specified.) Let v be a fixed real number no smaller than and let 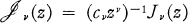if z ≠ 0 and 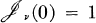, where Jv, is the Bessel function of the first kind of order v and cv =[2vΓ(v + 1)]–1; 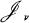is an entire function, as can be seen from the power series definition of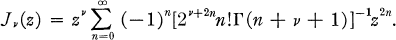

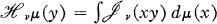The Hankel-Stieltjes transform of order v is given by .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 2 , April 1971 , pp. 236 - 246
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Bochner, S. and Chandrasekharan, K., Fourier transforms, Annals of Mathematics Studies, no. 19 (Princeton Univ. Press, Princeton, N.J.; Oxford Univ. Press, London, 1949).Google Scholar
2. Godement, R., Théorèmes taubériens et théorie spectrale, Ann. Sci. Ecole Norm. Sup. 64 (1947), 119–138.Google Scholar
3. Loomis, L. H., An introduction to abstract harmonie analysis (Van Nostrand, Princeton, N.J., 1953).Google Scholar
4. Reiter, H. J., Contributions to harmonie analysis. IV, Math. Ann. 135 (1958), 467–476.Google Scholar
5. Rudin, W., Representation of functions by convolutions, J. Math. Mech. 7 (1958), 103–115.Google Scholar
6. Rudin, W., Fourier analysis on groups, Interscience Tracts in Pure and Applied Mathematics, no. 12 (Interscience, New York, 1962).Google Scholar
7. Schwartz, A., The smoothness of Hankel transforms, J. Math. Anal. Appl. 28 (1969), 500–507.Google Scholar
8. Schwartz, L., Sur une propriété de synthèse spectrale dans les groupes non compacts, C. R. Acad. Sci. Paris 227 (1948), 424–426.Google Scholar
9. Watson, G. N., A treatise on the theory of Bessel functions (Cambridge Univ. Press, London, 1966).Google Scholar