Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chacron, M
1977.
Algebraic Φ-rings extensions of bounded index.
Journal of Algebra,
Vol. 44,
Issue. 2,
p.
370.
Giambruno, Antonino
1978.
Algebraic conditions on rings with involution.
Journal of Algebra,
Vol. 50,
Issue. 1,
p.
190.
Andrunakievich, V. A.
Arnautov, V. I.
Goyan, I. M.
and
Ryabukhin, Yu. M.
1980.
Associative rings.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
922.
Bell, H. E.
1980.
On commutativity of periodic rings and near-rings.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 36,
Issue. 3-4,
p.
293.
Bien, M. H.
Hai, B. X.
and
Hue, D. T.
2022.
On the unit groups of rings with involution.
Acta Mathematica Hungarica,
Vol. 166,
Issue. 2,
p.
432.


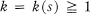 and some polynomial
and some polynomial 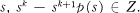 . What can one hope to say about such rings? Certainly all rings in which every symmetric element is nilpotent fall into this class.
. What can one hope to say about such rings? Certainly all rings in which every symmetric element is nilpotent fall into this class.