As part of their study of βω — ω and βω1 — ω1, A. Szymanski and H. X. Zhou [3] were able to exploit the following difference between ω, and ω: ω1, contains uncountably many disjoint sets whereas any uncountable family of subsets of ω is, at best, almost disjoint. To translate this distinction between ω1, and ω to a possible distinction between βω1 — ω1, and βω — ω they used the fact that if 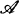a pairwise disjoint family of sets and a subset of each member of 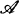is chosen then it is trivial to find a single set whose intersection with each member 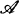is the chosen set. However, they noticed, it is not clear that the same is true if 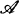is only a pairwise almost disjoint family even if we only require equality except on a finite set. But any homeomorphism from βω1 — ω1 to βω — ω would have to carry a disjoint family of subsets of ω1, to an almost disjoint family of subsets of ω with this property. This observation should motivate the following definition.