Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:16:55.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly Oscillatory and Nonoscillatory Subspaces of Linear Equations

Published online by Cambridge University Press:  20 November 2018

J. Michael Dolan  and
Gene A. Klaasen
J. Michael Dolan
Affiliation:
Oak Ridge National Laboratory, Operated by Union Carbide Corporation for the U.S. Atomic Energy Commission, Oak Ridge, Tennessee
Gene A. Klaasen
Affiliation:
University of Tennessee, Knoxville, Tennessee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the nth order linear equation

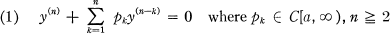
and particularly the third order equation

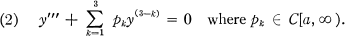
A nontrivial solution of (1)n is said to be oscillatory or nonoscillatory depending on whether it has infinitely many or finitely many zeros on [a, ∞). Let 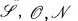denote respectively the set of all solutions, oscillatory solutions, nonoscillatory solutions of (1)n. 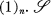is an n-dimensional linear space. A subspace is said to be nonoscillatory or strongly oscillatory respectively if every nontrivial solution of 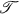is nonoscillatory or oscillatory. If 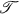contains both oscillatory and nonoscillatory solutions then 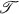is said to be weakly oscillatory.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 106 - 110
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Barrett, J. H., Oscillation theory of ordinary linear differential equations, Advances in Math. 3 (1969), 415–509.Google Scholar
2. Dolan, J. M., On the relationships between the oscillatory behavior of a linear third-order differential equation and its adjoint, J. Differential Equations 7 (1970), 367–388.Google Scholar
3. Dolan, J. M. and Klaasen, G., Dominance of nth order linear equations, Rocky Mountain Math, J., (to appear).Google Scholar
4. Hanan, M., Oscillation criteria for third-order linear differential equations, Pacific J. Math. 11 (1961), 919–944.Google Scholar
5. Jones, G., A property of y'” + p(x)y’ + 1/2 p‘(x)y = 0, Proc. Amer. Math. Soc. 33 (1972), 420–422.Google Scholar
6. Jones, G., Oscillation properties of third order differential equations, Rocky Mountain J. Math. (to appear).Google Scholar
7. Kondrat'ev, V., On the oscillation of solutions of linear differential equations of third and fourth order (in Russian), Trudy Moskov. Mat. Obsc. 8 (1959), 259–282.Google Scholar
8. Lazer, A., The behavior of solutions of the differential equation y'” + p(x)y = 0, Pacific J. Math. 17 (1966), 435–466.Google Scholar
9. Shaefer, H. H., Topological vector spaces (Macmillan Co., New York, 1966).Google Scholar
10. Swanson, C., Comparison and oscillation theory of linear differential equations (Academic Press, New York, London, 1968).Google Scholar
11. Utz, W., The nonoscillation of a solution of a third order equation, SIAM J. Math. Anal. 1 (1970), 535–537.Google Scholar
12. Utz, W., Oscillating solutions of third order differential equations, Proc. Amer. Math. Soc. 26 (1970), 273–276.Google Scholar
13. Valentine, F., Convex sets (McGraw-Hill Co., New York, 1964).Google Scholar