Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T02:26:00.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong Logarithmic Sobolev Inequalities for Log-Subharmonic Functions

Published online by Cambridge University Press:  20 November 2018

Piotr Graczyk ,
Todd Kemp  and
Jean-Jacques Loeb
Piotr Graczyk
Affiliation:
Université d'Angers, 2 Boulevard Lavoisier, 49045 Angers Cedex 01, France. e-mail: [email protected]
Todd Kemp
Affiliation:
Department of Mathematics, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA. e-mail: [email protected]
Jean-Jacques Loeb
Affiliation:
Université d'Angers, 2 Boulevard Lavoisier, 49045 Angers Cedex 01, France. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove an intrinsic equivalence between strong hypercontractivity and a strong logarithmic Sobolev inequality for the cone of logarithmically subharmonic (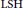$\text{LSH}$) functions. We introduce a new large class of measures, Euclidean regular and exponential type, in addition to all compactly-supported measures, for which this equivalence holds. We prove a Sobolev density theorem through 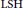$\text{LSH}$ functions and use it to prove the equivalence of strong hypercontractivity and the strong logarithmic Sobolev inequality for such log-subharmonic functions.

Keywords

47D06logarithmic Sobolev inequalities
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 6 , 01 December 2015 , pp. 1384 - 1410
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Anderson, G., Guionnet, A., and Zeitouni, O., An introduction to random matrices. Cambridge Studies in Advanced Mathematics, 118, Cambridge University Press, Cambridge, 2010.Google Scholar
[2] Bakry, D., L'hypercontractivité et son utilisation en théorie des semigroupes. In: Lectures on probability theory (Saint-Flour, 1992), Lecture Notes in Math., 1581, Springer, Berlin, 1994, pp. 1–114.Google Scholar
[3] Bakry, D., On Sobolev and logarithmic Sobolev inequalities true for Markov semigroups. In: New trends in stochastic analysis (Charingworth, 1994), World Sci. Publ., River Edge, NJ, 1997, pp. 43–75.Google Scholar
[4] Bakry, D. and Emery, M., Diffusions hypercontractives. Séminaire de Probabilités, XIX, Lecture Notes in Math. 1123, Springer, Berlin, 1985, pp. 177–206.Google Scholar
[5] Bobkov, S. and Houdré, C., Some connections between isoperimetric and Sobolev-type inequalities. Mem. Amer. Math. Soc. 129(1997), no. 616.Google Scholar
[6] Bobkov, S. and Ledoux, M., From Brunn-Minkowski to Brascamp-Lieb and to logarithmic Sobolev inequalities. Geom. Funct. Anal. 10(2000), no. 5, 1028–1052.http://dx.doi.Org/10.1007/PL00001645 Google Scholar
[7] Bobkov, S. and Tetali, P., Modified logarithmic Sobolev inequalities in discrete settings. J. Theoret. Probab. 19(2006), no. 2, 289–336.http://dx.doi.Org/10.1007/s10959-006-0016-3 Google Scholar
[8] Davies, E. B., Explicit constants for Gaussian upper bounds on heat kernels. Amer. J. Math. 109(1987), no. 2, 319–333.http://dx.doi.Org/10.2307/2374577 Google Scholar
[9] Davies, E. B., Heat kernels and spectral theory. Cambridge Tracts in Mathematics, 92, Cambridge University Press, Cambridge, 1990.Google Scholar
[10] Davies, E. B. and Simon, B., Ultracontractivity and the heat kernel for Schrödinger operators and Dirichlet Laplacians. J. Funct. Anal. 59(1984), no. 2, 335–395.http://dx.doi.Org/10.1016/0022-1236(84)90076-4 Google Scholar
[11] Diaconis, P. and Saloff-Coste, L., Logarithmic Sobolev inequalities for finite Markov chains. Ann. Appl. Probab. 6(1996), no. 3, 695–750.http://dx.doi.Org/10.1214/aoap/1034968224 Google Scholar
[12] Galaz-Fontes, F., Gross, L., and Sontz, S. B., Reverse hypercontractivity over manifolds. Ark. Math. 39(2001), no. 2, 283–309.http://dx.doi.Org/10.1007/BF02384558 Google Scholar
[13] Graczyk, P., Kemp, T., and Loeb, J.-J., Hypercontractivity for log-subharmonic functions. J. Funct. Anal. 258(2010), no. 6, 1785–1805.http://dx.doi.Org/10.1016/j.jfa.2009.08.014 Google Scholar
[14] Greene, R. and Krantz, S., Function theory of one complex variable. Third ed., Graduate Studies in Mathematics, 40, American Mathematical Society, Providence, RI, 2006.Google Scholar
[15] Gross, L., Logarithmic Sobolev inequalities. Amer. J. Math. 97(1975), no. 4, 1061–1083.http://dx.doi.Org/10.2307/2373688 Google Scholar
[16] Gross, L., Hypercontractivity over complex manifolds. Acta Math. 182(1999), no. 2, 159–206.http://dx.doi.org/10.1007/BF02392573 Google Scholar
[17] Gross, L. and Grothaus, M., Reverse hypercontractivity for subharmonic functions. Canad. J. Math. 57(2005), no. 3, 506–534.http://dx.doi.org/10.4153/CJM-2005-022-2 Google Scholar
[18] Guionnet, A. and Zegarlinski, B., Lectures on logarithmic Sobolev inequalities. Séminaire de Probabilités, XXXVI, Lecture Notes in Math., Springer, Berlin, 2003, pp. 1–134.Google Scholar
[19] Holley, R. and Stroock, D., Logarithmic Sobolev inequalities and stochastic Ising models. J. Statist. Phys. 46(1987), lno. 5–6, 159–1194.http://dx.doi.Org/10.1007/BF01011161 Google Scholar
[20] Janson, S., On hypercontractivity for multipliers of orthogonal polynomials. Ark. Mat. 21(1983), no. 1, 97–110.http://dx.doi.Org/10.1007/BF02384302 Google Scholar
[21] Janson, S., On complex hypercontractivity. J. Funct. Anal. 151(1997), no. 1, 270–280.http://dx.doi.org/10.1006/jfan.1997.3144 Google Scholar
[22] Ledoux, M., Isoperimetry and Gaussian analysis. In: Lectures on probability theory and statistics, Lecture Notes in Math 1648, Springer, Berlin, 1996, pp. 165–294.Google Scholar
[23] Ledoux, M., Concentration of measure and logarithmic Sobolev inequalities. Séminaire de Probabilités, XXXIII, Lecture Notes in Math., 1709, Springer, Berlin, 1999, pp. 120–216.Google Scholar
[24] Ledoux, M., The geometry of Markov diffusion generators. Ann. Fac. Sci. Toulouse Math. (6) 9(2000), no. 2, 305–366.http://dx.doi.Org/10.58O2/afst.962 Google Scholar
[25] Ledoux, M., The concentration of measure phenomenon. Mathematical Surveys and Monographs, 89, American Mathematical Society, Providence, RI, 2001.Google Scholar
[26] Ledoux, M., A remark on hypercontractivity and tail inequalities for the largest eigenvalues of random matrices. Séminaire de Probabilités XXXVII, Lecture Notes in Math., 1832, Springer, Berlin,2003, pp. 360–369.Google Scholar
[27] Ledoux, M., Spectral gap, logarithmic Sobolev constant, and geometric bounds. In: Surveys in differential geometry. Vol. IX, Surv. Differ. Geom., IX, Int. Press, Somerville, MA, 2004, pp. 219–240.Google Scholar
[28] Lelong, P. and Gruman, L., Entire functions of several complex variables. Grundlehren der Mathematischen Wissenschaften, 282, Springer-Verlag, Berlin, 1986.Google Scholar
[29] Nelson, E., The free Markov field. J. Funct. Anal. 12(1973), 211–227.http://dx.doi.Org/10.1016/0022-1236(73)90025-6 Google Scholar
[30] Stam, A. J., Some inequalities satisfied by the quantities of information of Fisher and Shannon. Information and Control 2(1959), 101–112.http://dx.doi.Org/10.1016/S0019-9958(59)90348-1 Google Scholar
[31] Villani, C., Topics in optimal transportation. Graduate Studies in Mathematics, 58, American Mathematical Society, Providence, RI, 2003.Google Scholar
[32] Yau, H.-T., Logarithmic Sobolev inequality for the lattice gases with mixing conditions. Commun. Math. Phys. 181(1996), no. 2, 367–408.http://dx.doi.org/10.1007/BF02101009 Google Scholar
[33] Yau, H.-T., Logorithmic Sobolev inequality for generalized simple exclusion processes. Probab. Theory Related Fields 109(1997), no. 4, 507–538.http://dx.doi.Org/10.1007/s004400050140 Google Scholar
[34] Zegarlinski, B., Dobrushin uniqueness theorem and logarithmic Sobolev inequalities. J. Funct. Anal. 105(1992), no. 1, 77–111. http://dx.doi.org/10.1016/0022-1236(92)90073-R Google Scholar
[35] Zimmermann, D., Logarithmic Sobolev inequalities for mollified compactly supported measures. J. Funct. Anal. 265(2013), no. 6, 1064–1083.http://dx.doi.Org/10.1016/i.ifa.2013.05.029 Google Scholar