Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-30T08:13:40.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong Converse Inequalities for Averages in Weighted Lp Spaces on [-1,1]

Published online by Cambridge University Press:  20 November 2018

M. Felten
M. Felten*
Affiliation:
Universität Dortmund, Mathematik VIII, D-44221 Dortmund, Germany email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Averages in weighted spaces 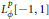$L_{\phi }^{p}[-1,1]$ defined by additions on 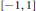$[-1,\,1]$ will be shown to satisfy strong converse inequalities of type $\text{A}$ and $\text{B}$ with appropriate 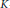$K$-functionals. Results for higher levels of smoothness are achieved by combinations of averages. This yields, in particular, strong converse inequalities of type 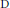$\text{D}$ between 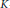$K$-functionals and suitable difference operators.

Keywords

41A2541A63averagesK-functionalsweighted spacesstrong converse inequalities
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 546 - 565
Copyright
Copyright © Canadian Mathematical Society 1999

References

[Di-Fe] Ditzian, Z. andFelten, M., Averages using translation induced by Laguerre and Jacobi expansions. Constr. Approx., to appear.Google Scholar
[Di-Iv] Ditzian, Z. and Ivanov, K., Strong converse inequalities. J. Anal. Math.. 61 (1993), 61–111.Google Scholar
[Di-Ru] Ditzian, Z. and Runovskii, K., Averages and K-functionals related to the Laplacian. J. Approx. Theory, to appear.Google Scholar
[Fe1] Felten, M., A Smoothness Concept forWeighted Lp Spaces on[−1; 1] Acta Sci.Math.. 62 (1996), 217–230.Google Scholar
[Fe2] Felten, M., A modulus of smoothness based on an algebraic addition. Aequationes Math.. 54 (1997), 56–73.Google Scholar
[Fe3] Felten, M., Characterization of best algebraic approximation by an algebraic modulus of smoothness. J. Approx. Theory. 89 (1997), 1–25.Google Scholar