Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-16T22:43:37.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Strict Comparison of Positive Elements in Multiplier Algebras

Published online by Cambridge University Press:  20 November 2018

Victor Kaftal ,
Ping Wong Ng  and
Shuang Zhang
Victor Kaftal
Affiliation:
Department of Mathematics, University of Cincinnati, P. O. Box 210025, Cincinnati, OH, 45221-0025, USA e-mail: [email protected]
Ping Wong Ng
Affiliation:
Department of Mathematics, University of Louisiana, 217 Maxim D. Doucet Hall, P.O. Box 43568 Lafayette, Louisiana, 70504-3568, USA e-mail: [email protected]
Shuang Zhang
Affiliation:
Department of Mathematics, University of Cincinnati, P.O. Box 210025, Cincinnati, OH, 45221-0025, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Main result: If a 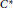${{C}^{*}}$-algebra 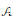$\mathcal{A}$ is simple, $\sigma $-unital, has finitely many extremal traces, and has strict comparison of positive elements by traces, then its multiplier algebra 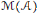$\mathcal{M}\left( \mathcal{A} \right)$ also has strict comparison of positive elements by traces. The same results holds if finitely many extremal traces is replaced by quasicontinuous scale. A key ingredient in the proof is that every positive element in the multiplier algebra of an arbitrary $\sigma $-unital 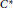${{C}^{*}}$ -algebra can be approximated by a bi-diagonal series. As an application of strict comparison, if 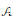$\mathcal{A}$ is a simple separable stable 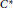${{C}^{*}}$ -algebra with real rank zero, stable rank one, and strict comparison of positive elements by traces, then whether a positive element is a positive linear combination of projections is determined by the trace values of its range projection.

Keywords

46L0546L3546L4547C15strict comparisonbi-diagonal formpositive combinations
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 2 , 01 April 2017 , pp. 373 - 407
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Blackadar, B., Comparison theory for simple C* -algebras. London Math. Soc Lecture Note Ser. 135. Cambridge University Press, Cambridge, 1988, pp. 21–54.Google Scholar
[2] Blackadar, B. and Handelman, D., Dimension functions and traces on C* -algebras. J. Funct. Anal. 45(1982), 297–340. http://dx.doi.org/10.1016/0022-1236(82)9009-X Google Scholar
[3] Brown, L. G., Stable isomorphism of hereditary subalgebras of C* -algebras. Pacific J. Math, 71(1977), 335–348. http://dx.doi.org/10.2140/pjm.1977.71.335 Google Scholar
[4] Brown, L. G.,Interpolation by projections in C* - algebras of real rank zero. J. Operator Theory 26(1991), no. 2, 383–387.Google Scholar
[5] Brown, L. G. and Pedersen, G. K. , C* -algebras of real rank zero. J. Funct. Anal. 99(1991), 131–149. http://dx.doi.Org/10.1016/0022-1236(91)90056-B Google Scholar
[6] Combes, F., Poids sur une C* -alg ébre. J. Math. Pures Appl. 47(1968) 57–100.Google Scholar
[7] Cuntz, J., Dimension functions on simple C* -algebras. Math. Ann. 233(1978), 145–153. http://dx.doi.org/10.1007/BF01421922 Google Scholar
[8] Dixmier, J., Les Algébres d'opérateurs dans l'espace hilbertien. 2nd ed. Gauthier-Villars, Paris, 1969.Google Scholar
[9] Dykema, K., Freeman, D., Kornelson, K.,Larson, D., Ordower, M., and Weber, E., Ellipsoidal tight frames and projection decompositions of operators. Illinois J. Math. 48(2004), 477–489.Google Scholar
[10] Elliott, G. A., Derivations of matroid C* -algebras. II. Ann. of Math. 100(1974), 407–422. http://dx.doi.Org/10.2307/1971079 Google Scholar
[11] Elliott, G. A. and Handelman, D. E., Addition of C* -algebra extensions. Pacific J. Math. 137(1989),no. 1, 87–121. http://dx.doi.org/10.2140/pjm.1989.137.87 Google Scholar
[12] Elliott, G. A. and Kucerovsky, D., An abstract Voiculescu-Brown-Douglas-Fillmore absorption theorem. Pacific J. Math. 198(2001), no. 2, 385–409. http://dx.doi.Org/10.2140/pjm.2001.198.385 Google Scholar
[13] Elliott, G., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a C* -algebra. Amer. J. Math. 133(2011), no. 4, 969–1005. http://dx.doi.org/10.1353/ajm.2o11.0027 Google Scholar
[14] Pack, T. and de la Harpe, P., Sommes de commutateurs dans les algebres de von Neumann finies continues. Ann. Inst. Fourier (Grenoble) 30(1980), 49–73.http://dx.doi.Org/10.5802/aif.792 Google Scholar
[15] Fillmore, P. A., Sums of operators with square zero. Acta Sci. Math. (Szeged), 28(1967), 285–288.Google Scholar
[16] Fong, C. K. and Murphy, G. J., Averages of projections. J. Operator Theory 13(1985), no. 2, 219–225.Google Scholar
[17] Goldstein, S. and Paszkiewicz, A., Linear combinations of projections in von Neumann algebras. Proc. Amer. Math. Soc. 116(1992), no. 1,175–183. http://dx.doi.org/10.1090/S0002-9939-1992-1094501-9 Google Scholar
[18] Goodearl, K. R., Partially ordered abelian groups with interpolation. Mathematical Surveys and Monographs, 20. American Mathematical Society, Providence, RI, 1986.Google Scholar
[19] Halpern, H., Kaftal, V., Ng, P. W., and Zhang, S., Finite sums of projections in von Neumann algebras. Trans. Amer. Math. Soc. 365(2013), 2409–2445. http://dx.doi.org/10.1090/S0002-9947-2013-05683-8 Google Scholar
[20] Kaftal, V., Ng, P. W., and Zhang, S., Strong sums of projections in von Neumann factors. J. Funct. Anal. 257(2009), no. 8, 2497–2529. http://dx.doi.Org/10.1016/j.jfa.2009.05.027 Google Scholar
[21] Kaftal, V., Positive combinations and sums of projections in purely infinite simple C* -algebras and their multiplier algebras. Proc. Amer. Math. Soc. 139(2011), no 8, 2735–2746. http://dx.doi.Org/10.1090/S0002-9939-2011-10995-XGoogle Scholar
[22] Kaftal, V., Positive combinations of projections in von Neumann algebras and purely infinite simple C* -algebras. Sci. China Math. 54(2011), no. 11, 2383–2393. http://dx.doi.org/10.1007/s11425-011-4253-2 Google Scholar
[23] Kaftal, V., Projection decomposition in multiplier algebras. Math. Ann. 352(2012), no 3, 543–566. http://dx.doi.org/10.1007/s00208-011-0649-0 Google Scholar
[24] Kaftal, V., Finite sums of projections in purely infinite simple C* -algebras with torsion K0. Proc. Amer. Math. Soc. 140(2012), no 9, 3219–3227. http://dx.doi.Org/10.1090/S0002-9939-2012-11152-9 Google Scholar
[25] Kaftal, V., Commutators and linear spans of projections in certain finite C* - algebras. J. Funct. Anal. 266(2014), no. 4, 1883–1912. http://dx.doi.Org/10.1016/j.jfa.2O13.12.009 Google Scholar
[26] Kaftal, V., Strict comparison of projections and positive combinations of projections in certain multiplier algebras. J. Oper. Theory (2015)73, no. 1,187–210. http://dx.doi.org/10.7900/jot.2013nov05.2014 Google Scholar
[27] Kucerovsky, D., Ng, P. W., and Perera, F., Purely infinite corona algebras of simple C* - algebras. Math. Ann. 346(2010), no. 1, 23–40. http://dx.doi.org/10.1007/s00208-009-0382-0 Google Scholar
[28] Kucerovsky, D. and Perera, F., Purely infinite corona algebras of simple C* -algebras with real rank zero J. Operator Theory 65(2011), no. 1,131–144.Google Scholar
[29] Laursen, K. B. and Sinclair, A. M., Lifting matrix units in C* -algebras. II. Math. Scand. 37(1975), no. 1, 167–172.Google Scholar
[30] Lin, H., Extensions by C* -algebras of real rank zero. III. Proc. London Math. Soc. 76(1998), no. 3, 634–666. http://dx.doi.Org/10.1112/S0024611598000355 Google Scholar
[31] Lin, H., Full extensions and approximate unitary equivalence. Pacific J. Math. 229(2007), no. 2, 389–428. http://dx.doi.org/10.2140/pjm.2007.229.389 Google Scholar
[32] Lin, H. and Ng, P. W., The corona algebra of the stabilized Jiang-Su algebra. J. Funct. Anal. 270(2016), no. 3,1220–1267. http://dx.doi.Org/10.1016/j.jfa.2O15.10.020 Google Scholar
[33] Marcoux, L. W., On the linear span of projections in certain simple C* -algebras. Indiana Univ. Math. J. 51(2002), no. 3, 753–771. http://dx.doi.org/10.1512/iumj.2002.51.2123 Google Scholar
[34] Marcoux, L. W., Sums of small number of commutators. J. Operator Theory 56(2006), no. 1,111–142.Google Scholar
[35] Marcoux, L. W., Projections, commutators and Lie ideals in C* -algebras. Math. Proc. R. Ir. Acad. 110A(2010), no. 1, 31–55.Google Scholar
[36] Marcoux, L. W. and Murphy, G. J., Unitarily-invariant linear spaces in C* -algebras. Proc. Amer. Math. Soc. 126(1998), 3597–3605. http://dx.doi.org/10.1090/S0002-9939-98-04934-X Google Scholar
[37] Matui, H. and Sato, Y., Strict comparison and Z-absorption of nuclear C* -algebras. Acta Math. 209(2012), no. 1, 179–196. http://dx.doi.Org/10.1007/s11511-012-0084-4 Google Scholar
[38] Ng, P. and Robert, L., Sums of commutators in pure C* -algebras. To appear in Munster J. Math. arxiv:1504.0046v1.Google Scholar
[39] Ortega, E., Rordam, M. and Thiel, H., The Cuntz semigroup and comparison of open projections. J. Funct. Anal. 260(2011), no. 12, 3474–3493. http://dx.doi.Org/10.1016/j.jfa.2O11.02.017 Google Scholar
[40] Pearcy, C. and Topping, D., Commutators and certain II1-factors. J. Funct. Anal. 3(1969), 69–78. http://dx.doi.Org/10.1016/0022-1236(69)90051-2 Google Scholar
[41] Pedersen, G. K., Measure theory for C* -algebras. Math. Scand. 19(1966), 131–145.Google Scholar
[42] Pedersen, G. K., C* -algebras and their automorphism groups. London Mathematical Society Monographs 14. Academic Press, London, 1979.Google Scholar
[43] Peligrad, C. and Zsido, L.. Open projections of C* -algebras comparison and regularity. In: Operator theoretical methods. Proceedings of the 17th international conference on operator theory, Timisoara, Romania, 1998. The Theta Foundation, Bucharest, 2000, pp. 285–300.Google Scholar
[44] Rordam, M., Ideals in the multiplier algebra of a stable C* -algebra. J. Operator Theory 25(1991), no. 2, 283–298.Google Scholar
[45] Rordam, M., On the structure of simple C* -algebras tensored with a UHF algebra. II. J. Funct. Anal. 107(1992), 255–269. http://dx.doi.org/10.1016/0022-1236(92)90106-S Google Scholar
[46] Rordam, M., The stable and the real rank of Z-absorbing C* -algebras. Internat. J. Math. 15(2004), no. 10, 1065–1084. http://dx.doi.org/10.1142/S0129167X04002661 Google Scholar
[47] Stratila, S. and Zsido, L., Lectures on von Neumann algebras. Abacus Press, Turnbridge Wells, 1975.Google Scholar
[48] Tikuisis, A. and Toms, A., On the structure ofCuntz semigroups in (possibly) nonunital C* -algebras. Canad. Math. Bull. 58(2015), no. 2, 402–414. http://dx.doi.org/10.4153/CMB-2014-040-5 Google Scholar
[49] Villadsen, J., Simple Ccalgebras with perforation. J. Funct. Anal. 154(1998), no. 1,110–116. http://dx.doi.org/10.1006/jfan.1997.3168 Google Scholar
[50] Winter, W., Nuclear dimension and Z-stability of pure C* - algebras. Invent. Math. 187(2012), no. 2, 259–342. http://dx.doi.org/10.1007/s00222-011-0334-7 Google Scholar
[51] Zhang, S., A Riesz decomposition property and ideal structure of multiplier algebras. J. Operator Theory 24(1990), 209–225.Google Scholar
[52] Zhang, S., Ki-groups, quasidiagonality, and interpolation by multiplier projections. Trans. Amer. Math. Soc. 325(1991), no. 2, 793–818.Google Scholar
[53] Zhang, S., Certain C* -algebras with real rank zero and their corona and multiplier algebras. I. Pacific J. Math. 155(1992), no. 1, 169–197. http://dx.doi.org/10.2140/pjm.1992.155.169 Google Scholar
[54] Zhang, S., Matricial structure and homotopy type of simple C* -algebras with real rank zero. J. Operator Theory 26(1991), no. 2, 283–312.Google Scholar