Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:42:11.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Fubini Theorem for Semimartingales in Hilbert Space

Published online by Cambridge University Press:  20 November 2018

Jorge A. León
Jorge A. León*
Affiliation:
Centro de Investigación y de Estudios Avanzandos, Departamento de Matemáticas, Apartado postal 14-740, México 07000 D. F., México
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we will study the Fubini theorem for stochastic integrals with respect to semimartingales in Hilbert space.

Let (Ω, 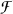, P) he a probability space, (X, 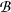, μ) a measure space, H and G two Hilbert spaces, L(H, G) the space of bounded linear operators from H into G, Z an H-valued semimartingale relative to a given filtration, and φ: X × R+ × Ω → L(H, G) a function such that for each t ∈ R+ the iterated integrals 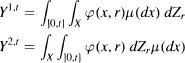are well-defined (the integrals with respect to μ are Bochner integrals). It is often necessary to have sufficient conditions for the process Y1 to be a version of the process Y2 (e.g. [1], proof of Theorem 2.11).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 5 , 01 October 1990 , pp. 890 - 901
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Bojdecki, T. and Gorostiza, L.G., Gaussian and non-Gaussian distribution-valuedOrnstein-Uhlenbeckprocesses , Rep. Int. 30 Depto. Matemáticas, CINVESTAV (1989).Google Scholar
2. Chojnowska-Michalik, A., Stochastic differential equations in Hilbert space and some of their applications, Ph.D. thesis, Institute of Mathematics, Polish Academy of Sciences (1976).Google Scholar
3. Chojnowska-Michalik, A., Stochastic differential equations in Hilbert space, Probability Theory- Banach Center Publications, 5 (1979), 53–74.Google Scholar
4. Curtain, R.F. and Falb, P.L., Stochastic differential equations in Hilbert space, J. Differential Equations 10 (1971), 412–430.Google Scholar
5. Gorostiza, L.G. and León, J.A., *-solutions of stochastic evolution equations in Hilbert space , Rep. Int. 29 Depto. Matemáticas, CINVESTAV (1989).Google Scholar
6. Hille, E. and Phillips, R.S., Functional analysis and semigroups, American Mathematical Society, Providence, Rhode Island(1957).Google Scholar
7. Ikeda, N. and Watanabe, S., Stochastic differential equations and diffusion processes, North-Holland Amsterdam-Oxford-New York (1981).Google Scholar
8. Jacod, J., Calcul stochastique et problèmes de martingales, Lee. Notes in Math. 714 Springer-Verlag Berlin-New York-Heidelberg (1979).Google Scholar
9. León, J.A., Stochastic evolution equations with respect to semimartingales in Hilbert space Stochastics27No. 1 (1989), 1–21.Google Scholar
10. Liptser, R.S. and Shiryayev, A.N., Statistics of random processes I. General theory, Springer-Verlag New York-Heidelberg-Berlin (1977).Google Scholar
11. Metivier, M., Semimartingales, W. de Gruyter, Berlin-New York (1982).Google Scholar
12. Walsh, , An introduction to stochastic partial differential equations, École d'Été de Probabilités de Saint Flour XIV-1984, Lee. Notes in Math. 1180, Springer-Verlag Berlin-Heidelberg-New York- Tokyo (1986).Google Scholar