Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T23:07:42.775Z Has data issue: false hasContentIssue false
  • English
  • Français

A Steinberg Cross Section for Non-Connected Affine Kac—Moody Groups

Published online by Cambridge University Press:  20 November 2018

Stephan Mohrdieck
Stephan Mohrdieck*
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstraße 55, 20146 Hamburg e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we generalise the concept of a Steinberg cross section to non-connected affine Kac–Moody groups. This Steinberg cross section is a section to the restriction of the adjoint quotient map to a given exterior connected component of the affine Kac–Moody group. (The adjoint quotient is only defined on a certain submonoid of the entire group, however, the intersection of this submonoid with each connected component is non-void.) The image of the Steinberg cross section consists of a “twisted Coxeter cell”, a transversal slice to a twisted Coxeter element. A crucial point in the proof of the main result is that the image of the cross section can be endowed with a 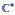${{\mathbb{C}}^{*}}$-action.

Keywords

22E67
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 625 - 642
Copyright
Copyright © Canadian Mathematical Society 2006

References

[Bo] Bourbaki, N., Groupes et algèbres de Lie. Chapitres 4–6. In: Éléments de mathématique. Actualits Scientifiques et Industrielles 1337, Hermann, Paris, 1968.Google Scholar
[Br] Brüchert, G., Trace class elements and cross sections in Kac-Moody groups. Canad. J. Math. 50(1998), no. 5, 972–1006.Google Scholar
[Co] Coleman, A. J., Killing and the Coxeter Transformation of Kac–Moody Algebras. Invent.Math. 95(1989), no. 3, 447–477.Google Scholar
[FM] Friedman, R. and Morgan, J. W., Holomorphic principal bundles over elliptic curves. II: The parabolic construction. J. Differential. Geom. 56(2000), no. 2, 301–379.Google Scholar
[FSS] Fuchs, J., Schellekens, B., and Schweigert, C., From Dynkin diagrams to fixed point structures. Comm. Math. Phys. 180(1996), no. 1, 39–97.Google Scholar
[Ga] Garland, H., The arithmetic theory of loop algebras. J. Algebra 53(1978), no. 2, 480–551.Google Scholar
[HS] Helmke, S. and Slodowy, P., Loop groups, principal bundles over elliptic curves and elliptic singularities. In: Geometry and Topology of Caustics. Banach Center Publication 62, Polish Acad. Sci., Warsaw, 2004.Google Scholar
[Hu] Humphreys, J. E., Reflection Groups and Coxeter Groups. Cambridge Studies in Advanced Mathematics 29, Cambridge University Press, Cambridge, 1990.Google Scholar
[Ja] Jantzen, J. C., Darstellungen halbeinfacher algebraischer Gruppen und zugeordnete kontravariante Formen. Bonn. Math. Schr. 67, 1973.Google Scholar
[Ka] Kac, V. G., Infinite Dimensional Lie Algebras. Third edition. Cambridge University Press, Cambridge, 1990.Google Scholar
[TL] Toledano Laredo, V., Positive energy representations of the loop groups of non-simply connected Lie groups. Comm. Math. Phys. 207(1999), no. 2, 307–339.Google Scholar
[Lo] Looijenga, E., Root systems and elliptic curves. Invent. Math. 38(1976/77), no. 1, 17–32.Google Scholar
[Moh] Mohrdieck, S., Conjugacy classes of non-connected semisimple algebraic groups. Transform. Groups, 8(2003), no. 4, 377–395.Google Scholar
[MW] Mohrdieck, S. and Wendt, R., Conjugacy Classes in Kac–Moody Groups and Principal G-Bundles over Elliptic Curves. In preparation.Google Scholar
[Mok1] Mokler, C.. The adjoint quotient for Kac-Moody groups. In preparation.Google Scholar
[Mok2] Mokler, C., On the Steinberg map and Steinberg cross-section for a symmetrizable indefinite Kac–Moody group. Canad. J. Math. 53(2001), no. 1, 195–211.Google Scholar
[Sc] Schweigert, C., On moduli spaces of flat connections with non-simply connected structure group. Nucl. Phys. B 492(1997), no. 3, 743–755.Google Scholar
[Sl] Slodowy, P., Simple Singularities and Simple Algebraic Groups. Lecture Notes in Mathematics 815, Springer, Berlin, 1980.Google Scholar
[Sp] Springer, T. A., Regular elements of finite reflection groups. Invent. Math. 25(1974), 159–198.Google Scholar
[St] Steinberg, R., Regular elements of semisimple algebraic groups. Inst. Hautes tudes Sci. Publ. Math. 25(1965), 49–80.Google Scholar
[We2] Wendt, R., A character formula for representations of loop groups based on non-simply connected Lie groups. Math. Z. 247(2004), no. 3, 549–580.Google Scholar