Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:32:20.693Z Has data issue: false hasContentIssue false
  • English
  • Français

The Stationary Phase Method for Certain Degenerate Critical Points I

Published online by Cambridge University Press:  20 November 2018

Milos Dostal  and
Bernard Gaveau
Milos Dostal
Affiliation:
Stevens Institute of Technology, Hoboken, New Jersey
Bernard Gaveau
Affiliation:
Université Pierre et Marie Curie, Paris, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider, in this work, the asymptotic behaviour for large λ, of a Fourier integral

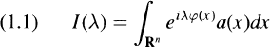
where 𝜑(x) is in general a C∞ function and a(x) a C∞ function with compact support. It is well known that the asymptotic behaviour of this integral is controlled by the behaviour of 𝜑 at its critical points (i.e., points where 𝜕𝜑/𝜕xj(x) = 0) and is given by local contributions at these points ([1], [3], [7], [9]).

In general, one assumes the hypothesis of non degenerate isolated critical point, namely that the determinant of the second derivative at the critical point is non zero.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 5 , 01 October 1989 , pp. 907 - 931
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Arnold, V., Varchenko, A.and Husein-Zadé, S., Singularités des applications différentiables 2, Monodromie, Mir (1986).Google Scholar
2. Atiyah, M., Resolution of singularities and division of distribution, Comm. pure and Applied Math. 23 (1970), 145–150.Google Scholar
3. Bleistein, N.and Handelsman, J., Asymptotic expansions of integrals (Holt, Rinehart, Winston, 1975).Google Scholar
4. Dostal, M.and Gaveau, B., Développements asymptotiques explicites d'intégrales de Fourier pour certains points critiques dégénérés, C.R. Acad. Sci. Paris 305 (1987), 857–859 et article détaillé à paraître.Google Scholar
5. Dostal, M.and Gaveau, B., Transformée de Fourier de certains corps convexes, C.R. Acad. Sci. Paris 307 (1988) et Bull. Sci. Math. (1989), to appear.Google Scholar
6. Dostal, M.and Macchia, R., Comportement asymptotique d'une intégrale de Fourier, Bull. Soc. Roy Sci. Liège 47 (1978), 12–16.Google Scholar
7. Erdelyi, A., Asymptotic expansions (Dover, 1956).Google Scholar
8. Jeanquartier, P., Développement asymptotique de la distribution de Dirac attachée à une fonction analytique, C.R. Acad. Sci. Paris 271, Série A (1970), 1159–1161.Google Scholar
9. Leray, J., Lagrangian analysis and quantum mechanics (MIT Press, 1980 et Cours au Collège de France, 1975–78).Google Scholar
10. Varchenko, A., Funct. Analysis i Prilo 10 (1976), 13–38.Google Scholar