Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:26:10.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Star Diagrams and the Symmetric Group

Published online by Cambridge University Press:  20 November 2018

R. A. Staal
R. A. Staal*
Affiliation:
University of New Brunswick
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

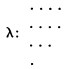Introduction. The irreducible representations of the symmetric group Sn, were shown by A. Young to be in one-to-one correspondence with certain arrays of n nodes. E.g. for n = 12 and the partition λ = [4, 4, 3, 1] we have the array which we call a “Young diagram.” The question arises as to the manner in which various properties of the representations are reflected in their corresponding Young diagrams.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 79 - 92
Copyright
Copyright © Canadian Mathematical Society 1950

References

[1] Brauer, R. and Nesbitt,, C , Ann. of Math., vol. 42 (1941), 556–590.Google Scholar
[2] Brauer, R. and Robinson, G. de B., Trans. Roy. Soc. Can., vol. XLI, series III, sec. III (1947), 11–25.Google Scholar
[3] Nakayama, T., Jap. J. Math., vol. 17 (1941), 411–423.Google Scholar
[4] Nakayama, T., Jap. J. Math., vol. 17 (1940), 165–184.Google Scholar
[5] Robinson, G. de B., Amer. J. Math., vol. LXX,(1948), 277–294.Google Scholar
[6] Robinson, G. Amer. J. Math., vol. LXIX, (1947), 286–298.Google Scholar