Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jarden, Moshe
1979.
An analogue of Artin-Schreier theorem.
Mathematische Annalen,
Vol. 242,
Issue. 3,
p.
193.
Madhan, Manohar L.
and
Madden, Daniel J.
1980.
On the theory of congruence function fields.
Communications in Algebra,
Vol. 8,
Issue. 17,
p.
1687.
Jarden, Moshe
1982.
The elementary theory of large e-fold ordered fields.
Acta Mathematica,
Vol. 149,
Issue. 0,
p.
239.
Fried, Michael D.
and
Jarden, Moshe
1986.
Field Arithmetic.
p.
248.
Geyer, Wulf-Dieter
and
Jarden, Moshe
1989.
On stable fields in positive characteristic.
Geometriae Dedicata,
Vol. 29,
Issue. 3,
p.
335.
Deveney, James K.
and
Yanik, Joe
1990.
Retracts of fields.
Archiv der Mathematik,
Vol. 55,
Issue. 5,
p.
445.
Geyer, Wulf-Dieter
Jarden, Moshe
and
Razon, Aharon
2017.
On stabilizers of algebraic function fields of one variable.
Advances in Geometry,
Vol. 17,
Issue. 2,
p.
131.


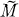 respectively the separable closure and the algebraic closure of M. If F is a variety which is defined over
respectively the separable closure and the algebraic closure of M. If F is a variety which is defined over 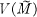 is dense in
is dense in 