Published online by Cambridge University Press: 20 November 2018
This paper starts by introducing a bi-periodic summation formula for automorphic forms on a group 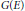 $G\left( E \right)$, with periods by a subgroup
$G\left( E \right)$, with periods by a subgroup 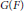 $G\left( F \right)$, where
$G\left( F \right)$, where 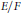 $E/F$ is a quadratic extension of number fields. The split case, where
$E/F$ is a quadratic extension of number fields. The split case, where 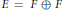 $E=F\oplus F$, is that of the standard trace formula. Then it introduces a notion of stable bi-conjugacy, and stabilizes the geometric side of the bi-period summation formula. Thus weighted sums in the stable bi-conjugacy class are expressed in terms of stable bi-orbital integrals. These stable integrals are on the same endoscopic groups
$E=F\oplus F$, is that of the standard trace formula. Then it introduces a notion of stable bi-conjugacy, and stabilizes the geometric side of the bi-period summation formula. Thus weighted sums in the stable bi-conjugacy class are expressed in terms of stable bi-orbital integrals. These stable integrals are on the same endoscopic groups 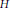 $H$ which occur in the case of standard conjugacy.
$H$ which occur in the case of standard conjugacy.
The spectral side of the bi-period summation formula involves periods, namely integrals over the group of  $F$-adele points of
$F$-adele points of  $G$, of cusp forms on the group of
$G$, of cusp forms on the group of  $E$-adele points on the group
$E$-adele points on the group  $G$. Our stabilization suggests that such cusp forms—with non vanishing periods—and the resulting bi-period distributions associated to “periodic” automorphic forms, are related to analogous bi-period distributions associated to “periodic” automorphic forms on the endoscopic symmetric spaces
$G$. Our stabilization suggests that such cusp forms—with non vanishing periods—and the resulting bi-period distributions associated to “periodic” automorphic forms, are related to analogous bi-period distributions associated to “periodic” automorphic forms on the endoscopic symmetric spaces 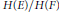 $H\left( E \right)/H\left( F \right)$. This offers a sharpening of the theory of liftings, where periods play a key role.
$H\left( E \right)/H\left( F \right)$. This offers a sharpening of the theory of liftings, where periods play a key role.
The stabilization depends on the “fundamental lemma”, which conjectures that the unit elements of the Hecke algebras on  $G$ and
$G$ and 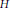 $H$ have matching orbital integrals. Even in stating this conjecture, one needs to introduce a “transfer factor”. A generalization of the standard transfer factor to the bi-periodic case is introduced. The generalization depends on a new definition of the factors even in the standard case.
$H$ have matching orbital integrals. Even in stating this conjecture, one needs to introduce a “transfer factor”. A generalization of the standard transfer factor to the bi-periodic case is introduced. The generalization depends on a new definition of the factors even in the standard case.
Finally, the fundamental lemma is verified for 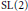 $\text{SL}\left( 2 \right)$.
$\text{SL}\left( 2 \right)$.