Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:57:35.406Z Has data issue: false hasContentIssue false
  • English
  • Français

The Square Sieve and the Lang–Trotter Conjecture

Published online by Cambridge University Press:  20 November 2018

Alina Carmen Cojocaru ,
Etienne Fouvry  and
M. Ram Murty
Alina Carmen Cojocaru
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, New Jersey, USA 08544, email: [email protected]
Etienne Fouvry
Affiliation:
Laboratoire de mathématiques, Université Paris-Sud Bât. 425, 9140 Orsay Cedex, France, CNRS UMR 8628, email [email protected]
M. Ram Murty
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Jeffery Hall, Kingston, Ontario, K7L 3N6, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

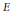Let $E$ be an elliptic curve defined over 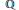$\mathbb{Q}$ and without complex multiplication. Let 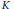$K$ be a fixed imaginary quadratic field. We find nontrivial upper bounds for the number of ordinary primes 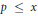$p\,\le \,x$ for which 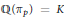$\mathbb{Q}\left( {{\pi }_{p}} \right)\,=\,K$, where 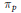${{\pi }_{p}}$ denotes the Frobenius endomorphism of 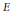$E$ at 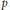$p$. More precisely, under a generalized Riemann hypothesis we show that this number is 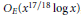${{O}_{E}}\left( {{x}^{17/18}}\,\log x \right)$, and unconditionally we show that this number is 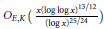${{O}_{E,K}}\left( \frac{x{{\left( \log \,\log x \right)}^{13/12}}}{{{\left( \log x \right)}^{25/24}}} \right)$ We also prove that the number of imaginary quadratic fields 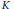$K$, with − disc 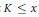$K\,\le \,x$ and of the form 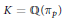$K\,=\,\mathbb{Q}({{\pi }_{p}})$, is 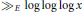${{\gg }_{E}}\,\log \,\log \,\log \,x$ for 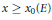$x\,\ge \,{{x}_{0}}\left( E \right)$. These results represent progress towards a 1976 Lang–Trotter conjecture.

Keywords

Primary: 11G05secondary: 11N3611R45Elliptic curves modulo pLang–Trotter conjectureapplications of sieve methods
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1155 - 1177
Copyright
Copyright © Canadian Mathematical Society 2005

References

[acC1] Cojocaru, A. C., Cyclicity of elliptic curves modulo p. PhD thesis, Queen's University, Kingston, Canada, 2002.Google Scholar
[acC2] Cojocaru, A. C., On the surjectivity of the Galois representations associated to non-CM elliptic curves. With an Appendix by Kani, E., Canad. Math. Bull.48(2005), 16–31.Google Scholar
[CM] Cojocaru, A. C. and Ram Murty, M., Introduction to Sieve Methods and Their Applications. LondonMathematical Society Student Texts, Cambridge University Press, Cambridge, 2005.Google Scholar
[El] Elkies, N. D., The existence of infinitely many supersingular primes for every elliptic curve over Q. Invent.Math. (3) 89(1987), 561–567.Google Scholar
[FM1] Fouvry, E. and Ram Murty, M., Supersingular primes common to two elliptic curves. London Math. Soc. Lecture Notes Series 215, Number Theory, Paris 1992–93 (ed., Sinnou, David), 1995, 91–102.Google Scholar
[FM2] Fouvry, E. and Ram Murty, M., On the distribution of supersingular primes. Canad. J. Math. (1) 48(1996), 81–104.Google Scholar
[H-B] Heath-Brown, D. R., The square sieve and consecutive square-free numbers. Math. Ann. 266(1984), 251–259.Google Scholar
[LO] Lagarias, J. and Odlyzko, A., Effective versions of the Chebotarev density theorem. In: Algebraic Number Fields, (ed., Fröhlich, A.), New York, Academic Press, 1977, 409–464.Google Scholar
[LT] Lang, S. and Trotter, H., Frobenius distributions in GL2-extensions. Lecture Notes in Math. 504, Springer Verlag, 1976.Google Scholar
[RM1] Ram Murty, M., An analogue of Artin's conjecture for abelian extensions. J. Number Theory (3) 18(1984), 241–248.Google Scholar
[RM3] Ram Murty, M., An introduction to Artin L-functions. J. RamanujanMath. Soc. (3) 16(2001), 261–307.Google Scholar
[MM] Ram Murty, M. and Kumar Murty, V., The Chebotarev density theorem and pair correlation of zeros of Artin L-functions, to be submitted.Google Scholar
[MMS] Ram Murty, M., Kumar Murty, V. and Saradha, N., Modular forms and the Chebotarev density theorem. Amer. J. Math. 110(1988), 253–281.Google Scholar
[Se1] Serre, J-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent.Math. 15(1972), 259–331.Google Scholar
[Se2] Serre, J-P., A course in arithmetic. Graduate Texts in Math. 7, Springer Verlag, 1996.Google Scholar
[Se3] Serre, J-P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 123–201.Google Scholar
[Se4] Serre, J-P., Collected papers. Volume III, Springer Verlag, 1985.Google Scholar
[Si1] Silverman, J. H., The arithmetic of elliptic curves. Graduate Texts in Math. 106, Springer Verlag, New York, 1986.Google Scholar
[Si2] Silverman, J. H., Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Math. 151, Springer Verlag, New York, 1994.Google Scholar
[St] Stark, H. M., Some effective cases of the Brauer-Siegel theorem. Invent.Math. 23(1974), 135–152.Google Scholar