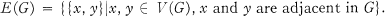Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Golumbic, Martin Charles
1980.
Algorithmic Graph Theory and Perfect Graphs.
p.
149.
Hammer, P. L.
Ibaraki, T.
and
Simeone, B.
1981.
Threshold Sequences.
SIAM Journal on Algebraic Discrete Methods,
Vol. 2,
Issue. 1,
p.
39.
West, Douglas B.
1982.
Ordered Sets.
p.
473.
Duchet, Pierre
1984.
Topics on Perfect Graphs.
Vol. 88,
Issue. ,
p.
67.
Nara, Chiê
and
Sato, Iwao
1984.
Split Graphs with Specified Dilworth Numbers.
Canadian Mathematical Bulletin,
Vol. 27,
Issue. 1,
p.
43.
Benzaken, C.
Hammer, P.L.
and
de Werra, D.
1985.
Split graphs of Dilworth number 2.
Discrete Mathematics,
Vol. 55,
Issue. 2,
p.
123.
Benzaken, C.
Hammer, P. L.
and
de Werra, D.
1985.
Threshold characterization of graphs with dilworth number two.
Journal of Graph Theory,
Vol. 9,
Issue. 2,
p.
245.
Tyshkevich, R. I.
and
Chernyak, A. A.
1985.
Decomposition of graphs.
Cybernetics,
Vol. 21,
Issue. 2,
p.
231.
West, Douglas B.
1985.
Graphs and Order.
p.
267.
Preissmann, M.
and
de Werra, D.
1985.
A note on strong perfectness of graphs.
Mathematical Programming,
Vol. 31,
Issue. 3,
p.
321.
Cochand, M.
and
de Werra, D.
1986.
Generalized neighbourhoods and a class of perfectly orderable graphs.
Discrete Applied Mathematics,
Vol. 15,
Issue. 2-3,
p.
213.
Cai, Leizhen
and
Maffray, Frédéric
1993.
On the SPANNING k-TREE problem.
Discrete Applied Mathematics,
Vol. 44,
Issue. 1-3,
p.
139.
Hammer, Peter L.
Mahadev, N.V.R.
and
Peled, Uri N.
1993.
Bipartite bithreshold graphs.
Discrete Mathematics,
Vol. 119,
Issue. 1-3,
p.
79.
1995.
Threshold Graphs and Related Topics.
Vol. 56,
Issue. ,
p.
513.
Golumbic, Martin Charles
2004.
Algorithmic Graph Theory and Perfect Graphs.
Vol. 57,
Issue. ,
p.
149.
Li, Rao
2009.
Finding Hamiltonian cycles in {quasi-claw,K1,5,K1,5+e}-free graphs with bounded Dilworth numbers.
Discrete Mathematics,
Vol. 309,
Issue. 8,
p.
2555.
Mukkamala, Padmini
Pach, János
and
Sarıöz, Deniz
2010.
Graph Theoretic Concepts in Computer Science.
Vol. 6410,
Issue. ,
p.
292.
Pach, János
and
Sarıöz, Deniz
2011.
On the Structure of Graphs with Low Obstacle Number.
Graphs and Combinatorics,
Vol. 27,
Issue. 3,
p.
465.
Berry, Anne
Brandstädt, Andreas
and
Engel, Konrad
2015.
The Dilworth Number of Auto-Chordal Bipartite Graphs.
Graphs and Combinatorics,
Vol. 31,
Issue. 5,
p.
1463.
Le, Van Bang
Oversberg, Andrea
and
Schaudt, Oliver
2016.
A unified approach to recognize squares of split graphs.
Theoretical Computer Science,
Vol. 648,
Issue. ,
p.
26.