Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T15:06:54.839Z Has data issue: false hasContentIssue false
  • English
  • Français

A splicing formula for the LMO invariant

Part of: Low-dimensional topology

Published online by Cambridge University Press:  20 August 2020

Gwénaël Massuyeau  and
Delphine Moussard
Gwénaël Massuyeau
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584, CNRS, Université Bourgogne Franche-Comté, 21000Dijon, France e-mail: [email protected]
Delphine Moussard*
Affiliation:
Institut de Mathématiques de Marseille, UMR 7373, Université d’Aix–Marseille, Marseille, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a “splicing formula” for the LMO invariant, which is the universal finite-type invariant of rational homology three-spheres. Specifically, if a rational homology three-sphere M is obtained by gluing the exteriors of two framed knots 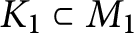$K_1 \subset M_1$ and 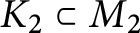$K_2\subset M_2$ in rational homology three-spheres, our formula expresses the LMO invariant of M in terms of the Kontsevich–LMO invariants of 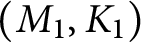$(M_1,K_1)$ and 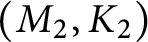$(M_2,K_2)$ . The proof uses the techniques that Bar-Natan and Lawrence developed to obtain a rational surgery formula for the LMO invariant. In low degrees, we recover Fujita’s formula for the Casson–Walker invariant, and we observe that the second term of the Ohtsuki series is not additive under “standard” splicing. The splicing formula also works when each 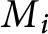$M_i$ comes with a link 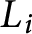$L_i$ in addition to the knot 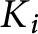$K_i$ , hence we get a “satellite formula” for the Kontsevich–LMO invariant.

Keywords

LMO invariantsplicinghomology sphereknotKontsevich–LMO invariantCasson–Walker invariantsurgeryJacobi diagram

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 6 , December 2021 , pp. 1743 - 1770
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research has been funded by the project “ITIQ-3D” of the Région Bourgogne Franche–Comté. G.M. is partly supported by the project “AlMaRe” (ANR-19-CE40-0001-01) and by the EIPHI Graduate School (ANR-17-EURE-0002).

References

Andersen, J., Mattes, J., and Reshetikhin, N., Quantization of the algebra of chord diagrams . Math. Proc. Camb. Philos. Soc. 124(1998), no. 3, 451–467.CrossRefGoogle Scholar
Barge, J. and Ghys, E., Cocycles d’Euler et de Maslov . Math. Ann. 294(1992), no. 2, 235–265.CrossRefGoogle Scholar
Bar-Natan, D., Garoufalidis, S., Rozansky, L., and Thurston, D., The Aarhus integral of rational homology 3-spheres II. Invariance and universality . Selecta Math. 8(2002), no. 3, 341–371.CrossRefGoogle Scholar
Bar-Natan, D., Garoufalidis, S., Rozansky, L., and Thurston, D., The Aarhus integral of rational homology 3-spheres. III. Relation with the Le-Murakami-Ohtsuki invariant . Selecta Math. 10(2004), no. 3, 305–324.CrossRefGoogle Scholar
Bar-Natan, D. and Lawrence, R., A rational surgery formula for the LMO invariant . Israel J. Math. 140(2004), 29–60.CrossRefGoogle Scholar
Bar-Natan, D., Le, T., and Thurston, D., Two applications of elementary knot theory to Lie algebras and Vassiliev invariants . Geom. Topol. 7(2003), 1–31.CrossRefGoogle Scholar
Boden, H. and Himpel, B., Splitting the spectral flow and the SU(3) Casson invariant for spliced sums . Alg. Geom. Topol. 9(2009), no. 2, 865–902.CrossRefGoogle Scholar
Boyer, S. and Nicas, A., Varieties of group representations and Casson’s invariant for rational homology 3-spheres . Trans. Am. Math. Soc. 322(1990), no. 2, 507–522.Google Scholar
Cochran, T. and Gompf, R., Applications of Donaldson’s theorems to classical knot concordance homology 3-spheres and property P . Topology 27(1988), no. 4, 495–512.CrossRefGoogle Scholar
Eisenbud, D. and Neumann, W., Three-dimensional link theory and invariants of plane curve singularities . Annals of Mathematics Studies, 110, Princeton University Press, Princeton, NJ, 1985.Google Scholar
Fujita, G., A splicing formula for Casson–Walker’s invariant . Math. Ann. 296(1993), no. 2, 327–338.CrossRefGoogle Scholar
Fukuhara, S. and Maruyama, N., A sum formula for Casson’s λ-invariant . Tokyo J. Math. 11(1988), no. 2, 281–287.CrossRefGoogle Scholar
Garoufalidis, S., Goussarov, M., and Polyak, M., Calculus of clovers and finite type invariants of 3-manifolds . Geom. Topol. 5(2001), 75–108.CrossRefGoogle Scholar
Ghys, E. and Ranicki, A., Signatures in algebra, topology and dynamics, Six papers on signatures, braids and Seifert surfaces. Ensaios Mat., 30, Sociedade Brasileira de Matematica, Rio de Janeiro, Brazil, 2016, pp. 1–173.Google Scholar
Gordon, C., Knots, homology spheres, and contractible 4-manifolds . Topology 14(1975), 151–172.CrossRefGoogle Scholar
Habiro, K., Claspers and finite type invariants of links . Geom. Topol. 4(2000), 1–83.CrossRefGoogle Scholar
Habiro, K. and Massuyeau, G., The Kontsevich integral for bottom tangles in handlebodies. Quan. Topol., to appear. arXiv:1702.00830v4Google Scholar
Ito, T., On LMO invariant constraints for cosmetic surgery and other surgery problems for knots in ${S}^3$ . Comm. Analysis Geom. 28 (2020), 321–349.Google Scholar
Kirby, R. and Melvin, P., Dedekind sums, $\mu$ -invariants and the signature cocycle . Math. Ann. 299(1994), no. 2, 231–267.CrossRefGoogle Scholar
Kricker, A., The lines of the Kontsevich integral and Rozansky’s rationality conjecture. Preprint, 2000. arXiv:math/0005284v1Google Scholar
Le, T., An invariant of integral homology 3-spheres which is universal for all finite type invariants . In: Solitons, geometry, and topology: On the crossroad, Amer. Math. Soc. Transl. Ser. 2, 179, American Mathematical Society, Providence, RI, 1997, pp. 75–100.Google Scholar
Le, T., Murakami, J., and Ohtsuki, T., On a universal perturbative invariant of 3-manifolds . Topology 37(1998), no. 3, 539–574.CrossRefGoogle Scholar
Massuyeau, G., Splitting formulas for the LMO invariant of rational homology three-spheres . Alg. Geom. Topol. 14(2014), no. 4, 3553–3588.CrossRefGoogle Scholar
Moussard, D., On Alexander modules and Blanchfield forms of null-homologous knots in rational homology spheres . J. Knot Th. Ramif. 21(2012), no. 5, 1250042, 21 pp.CrossRefGoogle Scholar
Moussard, D., Finite type invariants of rational homology 3-spheres . Alg. Geom. Topol. 12(2012), no. 4, 2389–2428.CrossRefGoogle Scholar
Ohtsuki, T., Finite type invariants of integral homology 3-spheres . J. Knot Th. Ramif. 5(1996), no. 1, 101–115.CrossRefGoogle Scholar
Ohtsuki, T., A polynomial invariant of rational homology 3-spheres . Invent. Math. 123(1996), no. 2, 241–257.CrossRefGoogle Scholar
Suetsugu, Y., Kontsevich invariant for links in a donut and links of satellite form . Osaka J. Undergrad. Math. 33(1996), no. 4, 823–828.Google Scholar
Walker, K., An extension of Casson’s invariant. Annals of Mathematics Studies, 126, Princeton University Press, Princeton, NJ, 1992.CrossRefGoogle Scholar