Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:44:23.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical Functions for the Semisimple Symmetric Pair (Sp(2, ℝ), SL(2, ℂ))

Published online by Cambridge University Press:  20 November 2018

Tomonori Moriyama
Tomonori Moriyama*
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, 3-8-1 Komaba Meguro-Ku, Tokyo 153-8914, Japan, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\pi $ be an irreducible generalized principal series representation of 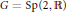$G\,=\,\text{Sp}\left( 2,\,\mathbb{R} \right)$ induced from its Jacobi parabolic subgroup. We show that the space of algebraic intertwining operators from $\pi $ to the representation induced from an irreducible admissible representation of 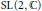$\text{SL}\left( 2,\,\mathbb{C} \right)$ in 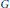$G$ is at most one dimensional. Spherical functions in the title are the images of 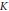$K$-finite vectors by this intertwining operator. We obtain an integral expression of Mellin-Barnes type for the radial part of our spherical function.

Keywords

22E4511F70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 4 , 01 August 2002 , pp. 828 - 865
Copyright
Copyright © Canadian Mathematical Society 2002

References

[B] Bump, D., Automorphic forms on GL(3; R). Lecture Notes in Math. 1083, Springer-Verlag, 1984.Google Scholar
[Er] Erdelyi, A. et al., Higher transcendental functions, vol. I. McGraw-Hill, 1953.Google Scholar
[H1] Hirano, M., Shintani functions on GL(2, R). Trans. Amer. Math. Soc. 352 (2000), 1709–1721.Google Scholar
[H2] Hirano, M., Shintani functions on GL(2, C). Trans. Amer. Math. Soc. 353 (2001), 1535–1550.Google Scholar
[H3] Hirano, M., Fourier-Jacobi type spherical functions for discrete series representations of Sp(2, R). Compositio Math. 128 (2001), 177–216.Google Scholar
[I] Ishii, T., Siegel-Whittaker functions on Sp(2, R) for principal series representations. Preprint, 2000.Google Scholar
[M-O] Miyazaki, T. and Oda, T., Principal series Whittaker functions on Sp(2, R) II. Tôhoku Math. J. 50 (1998), 243–260.Google Scholar
[Mo1] Moriyama, T., Spherical functions with respect to the semisimple symmetric pair (Sp(2, R), SL(2, R) × SL(2, R)). J. Math. Sci. Univ. Tokyo. 6 (1999), 127–179.Google Scholar
[Mo2] Moriyama, T., A remark on Whittaker functions on Sp(2, R). Submitted.Google Scholar
[M-S] Murase, A. and Sugano, T., Shintani function and its application to automorphic L-functions for classical groups I, the orthogonal group case. Math. Ann. 299 (1994), 17–56.Google Scholar
[N] Nörlund, N. E., Hypergeometric functions. Acta Math. 94 (1955), 289–349.Google Scholar
[R] Rossmann, W., The structure of semisimple symmetric spaces. Canad. J. Math. 31 (1979), 157–180.Google Scholar
[T1] Tsuzuki, M., Real Shintani functions and multiplicity free property for the symmetric pair (SU(2, 1), S(U(1, 1) × U(1))). J. Math. Sci. Univ. Tokyo. 4 (1997), 663–727.Google Scholar
[T2] Tsuzuki, M., Real Shintani functions on U(n, 1). J. Math. Sci. Univ. Tokyo. 8 (2001), 609–688.Google Scholar
[Wa] Wallach, N., Real reductive groups I. Academic Press, 1988.Google Scholar