Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T13:23:36.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Flow for Nonunital Spectral Triples

Published online by Cambridge University Press:  20 November 2018

A. L. Carey ,
V. Gayral ,
J. Phillips ,
A. Rennie  and
F. A. Sukochev
A. L. Carey
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra ACT, 0200 Australia and School of Mathematics and Applied Statistics, University of Wollongong, Wollongong NSW, 2500 Australia e-mail: [email protected], [email protected]
V. Gayral
Affiliation:
Laboratoire de Mathématiques, Université Reims Champagne-Ardenne, Moulin de la Housse-BP 1039, 51687 Reims France e-mail: [email protected]
J. Phillips
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria BC e-mail: [email protected]
A. Rennie
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra ACT, 0200 Australia and School of Mathematics and Applied Statistics, University of Wollongong, Wollongong NSW, 2500 Australia e-mail: [email protected], [email protected]
F. A. Sukochev
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Kensington NSW, 2052 Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

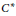We prove two results about nonunital index theory left open in a previous paper. The first is that the spectral triple arising from an action of the reals on a ${{C}^{*}}$-algebra with invariant trace satisfies the hypotheses of the nonunital local index formula. The second result concerns the meaning of spectral flow in the nonunital case. For the special case of paths arising from the odd index pairing for smooth spectral triples in the nonunital setting, we are able to connect with earlier approaches to the analytic definition of spectral flow.

Keywords

46H30spectral triplespectral flowlocal index theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 4 , 01 August 2015 , pp. 759 - 794
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Atiyah, M. F., Patodi, V. K., and Singer, I. M., Spectral asymmetry and Riemannian geometry. III. Math. Proc. Cambridge Philos. Soc. 79(1976), no. 1, 71–99.http://dx.doi.Org/10.1017/S0305004100052105 Google Scholar
[2] Benameur, M.-T., Carey, A. L., Phillips, J., Rennie, A., Sukochev, F. A., and Wojciechowski, K. P., An analytic approach to spectral flow in von Neumann algebras. In: Analysis, geometry and topology of elliptic operators, World Sci. Publ., Hackensack, NJ, 2006, pp. 297–352.Google Scholar
[3] Benameur, M.-T. and Fack, T. Type II noncommutative geometry. I. Dixmier trace in von Neumann algebras. Adv. Math. 199(2006), no. 1, 29–87.http://dx.doi.Org/10.1016/j.aim.2004.11.001 Google Scholar
[4] Breuer, M., Fredholm theories in von Neumann algebras. I. Math. Ann. 178(1968), 243–254.http://dx.doi.Org/10.1007/BF01350663 Google Scholar
[5] Breuer, M., Fredholm theories in von Neumann algebras. II. Math. Ann. 180(1969), 313–325.http://dx.doi.org/10.1007/BF01351884 Google Scholar
[6] Brown, L. G.and Kosaki, H., Jensen’s inequality in semifinite von Neumann algebras. J. Operator Theory 23(1990), 3–19.Google Scholar
[7] Carey, A. L., Gayral, V., Rennie, A., and Sukochev, F.A., Index theory for locally compact noncommutative geometries. Mem. Amer. Math. Soc. 231(2014), no. 1085.Google Scholar
[8] Carey, A. L. and Phillips, J., Unbounded Fredholm modules and spectral flow. Canad. J. Math. 50(1998), no. 4, 673–718. http://dx.doi.org/10.4153/CJM-1998-038-x Google Scholar
[9] Carey, A. L. and Phillips, J., Spectral flow in Θ–summable Fredholm modules, eta invariants and the JLO cocycle. J. iC–Theory 31(2004), no. 2, 135–194.http://dx.doi.Org/10.1023/B:KTHE.0000022922.68170.61 Google Scholar
[10] Carey, A. L., Phillips, J., Rennie, A., Sukochev, F. A., The local index formula in semifinite von Neumann algebras I. Spectral flow. Adv. Math. 202(2006), no. 2, 451–516.http://dx.doi.Org/10.1016/j.aim.2005.03.011 Google Scholar
[11] Carey, A. L., Phillips, J., Rennie, A., Sukochev, F. A., The local index formula in semifinite von Neumann algebras II: the even case. Adv. Math. 202(2006), no. 2, 517–554.http://dx.doi.Org/10.1016/j.aim.2005.03.010 Google Scholar
[12] Carey, A. L., Phillips, J., and Sukochev, F. A., Spectral flow and Dixmier traces. Adv. Math. 173(2003), 68–113.http://dx.doi.Org/10.1016/S0001-8708(02)00015-4 Google Scholar
[13] Connes, A., Noncommutative differential geometry. Publ. Math. Inst. Hautes Études Sci. 62(1985), 257–360.Google Scholar
[14] Connes, A. and Moscovici, H., The local index formula in noncommutative geometry. Geom. Funct. Anal. 5(1995), no. 2, 174–243.http://dx.doi.org/10.1007/BF01895667 Google Scholar
[15] Dixmier, J., Les algèbres d'opérateurs dans l'espace Hilbertien (Algèbres de von Neumann), Gauthier–Villars, Paris, 1969.Google Scholar
[16] Georgescu, M., Spectral flow in semi–finite von Neumann algebras.Ph.D. Thesis, University of Victoria, BC.Google Scholar
[17] Getzler, E., The odd Chern character in cyclic homology and spectral flow. Topology 32(1993),no. 3, 489–507.http://dx.doi.org/10.1016/0040-9383(93)90002-D Google Scholar
[18] Higson, N., The local index formula in noncommutative geometry. In: Contemporary developments in algebraic Jf–theory, ICTP Lecture Notes, 15, Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2004, pp. 444–536.Google Scholar
[19] Lesch, M., On the index of the infinitesimal generator of a flow. J. Operator Theory 26(1991), no. 1. 73–92.Google Scholar
[20] Pedersen, G. and Takesaki, M., The Radon–Nikodym theorem for von Neumann algebras. Acta Math. 130(1973), 53–87. http://dx.doi.org/10.1007/BF02392262 Google Scholar
[21] Phillips, J., Self–adjoint Fredholm operators and spectral flow. Canad. Math. Bull. 39(1996), no. 4, 460–467. http://dx.doi.org/10.4153/CMB-1996-054-4 Google Scholar
[22] Phillips, J., Spectral flow in type I and type II factors–a new approach. In: Cyclic cohomology and noncommutative geometry (Waterloo, ON, 1995), Fields Institute Commun., 17, American Mathematical Society, Providence, RI, 1997, pp. 137–153.Google Scholar
[23] Phillips, J. and Raeburn, Iain, An index theorem for Toeplitz operators with noncommutative symbol space. J. Funct. Anal. 120(1994), no. 2, 239–263.http://dx.doi.Org/10.1006/jfan.1994.1032 Google Scholar
[24] Singer, I. M., Eigenvalues of the Laplacian and invariants of manifolds. In: Proceedings of the International Congress of Mathematicians (Vancouver, BC, 1974), vol. 1, Canad. Math. Congress, Montreal, QC, 1975, pp. 187–200.Google Scholar