Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T13:22:44.952Z Has data issue: false hasContentIssue false
  • English
  • Français

A Space of Harmonic Maps from a Sphere into the Complex Projective Space

Published online by Cambridge University Press:  20 November 2018

Hiroko Kawabe
Hiroko Kawabe*
Affiliation:
Toin University of Yokohama, 1614, Kurogane-Cho, Aoba-Ku, Yokohama-Shi 225-8502, Japan, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Guest–Ohnita and Crawford have shown the path-connectedness of the space of harmonic maps from 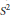${{S}^{2}}$ to 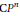$\text{C}{{P}^{n}}$ of a fixed degree and energy. It is well known that the $\partial$ transform is defined on this space. In this paper, we will show that the space is decomposed into mutually disjoint connected subspaces on which $\partial$ is homeomorphic.

Keywords

58E2058D15harmonic mapsharmonic sequencesgluing
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 879 - 904
Copyright
Copyright © Canadian Mathematical Society 2013

References

[CW] Chern, S. S. and G.Wolfson, J., Harmonic maps of the two-sphere into a complex Grassmann manifold II*. Ann. of Math. 125(1987), no. 2, 301–335. http://dx.doi.org/10.2307/1971312 Google Scholar
[C] Crawford, T. A., The space of harmonic maps from the 2-sphere to the complex projective plane. Canad. Math. Bull. 40(1997), no. 3, 285–295. http://dx.doi.org/10.4153/CMB-1997-035-4 Google Scholar
[EW] Eells, J. and Wood, J. C., Harmonic maps from surfaces to complex projective spaces. Adv. in Math. 49(1983), no. 3, 217–263. http://dx.doi.org/10.1016/0001-8708(83)90062-2 Google Scholar
[GH] Griffiths, P. and Harris, J., Principles of algebraic geometry. Pure and Applied Mathematics, Wiley-Interscience, New York, 1978. Google Scholar
[GO] Guest, M. A. and Ohnita, Y., Group actions and deformations for harmonic maps. J. Math. Soc. Japan 45(1993), no. 4, 671–704. http://dx.doi.org/10.2969/jmsj/04540671 Google Scholar
[K] Kawabe, H., Harmonic maps from the Riemann sphere into the complex projective space and the harmonic sequences. Kodai Math. J. 33(2010), no. 3, 367–382. http://dx.doi.org/10.2996/kmj/1288962548 Google Scholar
[KN] Kobayashi, S. and Nomizu, K., Foundations of differential geometry. Vol. I and Vol. II, JohnWiley & Sons, Inc., New York, 1996. Google Scholar
[LW1] Lemaire, L. and C.Wood, J., On the space of harmonic 2-spheres in CP2. Internat. J. Math. 7(1996), no. 2, 211–225. http://dx.doi.org/10.1142/S0129167X96000128 Google Scholar
[LW2] Lemaire, L., Jacobi fields along harmonic 2-spheres in CP2 are integrable. J. London Math. Soc. (2) 66(2002), no. 2, 468–486. http://dx.doi.org/10.1112/S0024610702003496 Google Scholar
[P] Parker, T. H., Bubble tree convergence for harmonic maps. J. Differential Geom. 44(1996), no. 3, 595–633.Google Scholar
[PW] Parker, T. H. and G.Wolfson, J., Pseudoholomorphic maps and bubble trees. J. Geom. Anal. 3(1993), no. 1, 63–98. http://dx.doi.org/10.1007/BF02921330 Google Scholar
[W] G.Wolfson, J., Harmonic sequences and harmonic maps of surfaces into complex Grassmann manifolds. J. Differential Geom. 27(1988), no. 1, 161–178. Google Scholar