Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T02:03:56.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Sommes friables d'exponentielles et applications

Published online by Cambridge University Press:  20 November 2018

Sary Drappeau
Sary Drappeau*
Affiliation:
Université Paris Diderot – Paris 7, Institut de Mathé matiques de Jussieu–Paris Rive Gauche, UMR 7586, Bâtiment Chevaleret, Bureau 7C08, 75205 Paris Cedex 13 courriel: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integer is said to be 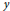$y$-friable if its greatest prime factor is less than 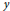$y$. In this paper, we obtain estimates for exponential sums over 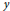$y$-friable numbers up to 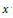$x$ which are non-trivial when 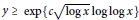$y\,\ge \,\exp \left\{ c \right.\sqrt{\log \,x\,}\log \,\log \,\left. x \right\}$. As a consequence, we obtain an asymptotic formula for the number of $y$-friable solutions to the equation 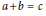$a\,+\,b\,=\,c$ which is valid unconditionally under the same assumption. We use a contour integration argument based on the saddle point method, as developped in the context of friable numbers by Hildebrand and Tenenbaum, and used by Lagarias, Soundararajan and Harper to study exponential and character sums over friable numbers.

Keywords

12N2511L07théorie analytique des nombresentiers friablesméthode du col
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 3 , 01 June 2015 , pp. 597 - 638
Copyright
Copyright © Canadian Mathematical Society 2015

References

[Dab75] Daboussi, H., Fonctions multiplicatives presque périodiques B. Astérisque 24-25(1975), 321–324.Google Scholar
[DM00] Davenport, H., Multiplicative number theory. Graduate Texts in Math. 6, Springer Verlag, New York, 2000.Google Scholar
[DB51] de Bruijn, N., On the number of positive integers ≤x and free of prime factors > y. Nederl. Akad.Wetensch 54(1951),50–60.+y.+Nederl.+Akad.Wetensch+54(1951),50–60.>Google Scholar
[dlB98] de la Bretèche, R., Sommes d'exponentielles et entiers sans grand facteur premier. Proc.London Math. Soc. 77(1998), 39–78. http://dx.doi.org/10.1112/S0024611598000409 Google Scholar
[dlB99] de la Bretèche, R., Sommes sans grand facteur premier. Acta Arith. 88(1999), 1–14.Google Scholar
[dlBG12] de la Bretèche, R. et Granville, A., Densité des friables. Bulletin de la SMF (2012), à paraître.Google Scholar
[dlBT05a] de la Bretèche, R. et Tenenbaum, G., Entiers friables: inégalité de Turán–Kubilius et applications. Invent. Math. 159(2005), 531–588.http://dx.doi.org/10.1007/s00222-004-0379-y Google Scholar
[dlBT05b] de la Bretèche, R. et Tenenbaum, G., Propriétés statistiques des entiers friables. Ramanujan J. 9(2005), 139–202. http://dx.doi.org/10.1007/s11139-005-0832-6 Google Scholar
[BHT82] Dupain, Y., Hall, R. R., et Tenenbaum, G., Sur l'équirépartition modulo 1 de certaines fonctions de diviseurs. J. London Math. Soc. 2(1982), 397.http://dx.doi.Org/10.1112/jlms/s2-26.3.397 Google Scholar
[Dral2] Drappeau, S., Sur les solutions friables de l'équation a + b = c. Math. Proc. Cambridge Phil. Soc, 2012, à paraître. http://dx.doi.Org/10.1017/S0305004112000643 Google Scholar
[FT91] Fouvry, E. et Tenenbaum, G., Entiers sans grand facteur premier en progressions arithmétiques. Proc. London Math. Soc. 3(1991), 449–494. http://dx.doi.Org/10.1112/plms/s3-63.3.449 Google Scholar
[GraO8] Granville, A., Smooth numbers: computational number theory and beyond. Math. Sci. Res. Inst. Publ. 44(2008), 267–323.Google Scholar
[Harl2a] Harper, A. J., On a paper of K. Soundararajan on smooth numbers in arithmetic progressions. J. Number Theory 132(2012), 182–199.http://dx.doi.Org/10.1016/j.jnt.2O11.07.005 Google Scholar
[Harl2b] Harper, A. J., Bombieri–Vinogradov and Barban–Davenport–Halberstam type theorems for smooth numbers. arxiv:1208.5992Google Scholar
[Hil85] Hildebrand, A., Integers free of large prime divisors in short intervals. Quart. J. Math. Oxford 36(1985), 57–69.http://dx.doi.Org/10.1093/qmath/36.1.57 Google Scholar
[HT86] Hildebrand, A. et Tenenbaum, G., On integers free of large prime factors. Trans. Amer. Math. Soc. 296(1986), 265–290.http://dx.doi.org/10.1090/S0002-9947-1986-0837811-1 Google Scholar
[HT93] Hildebrand, A. et Tenenbaum, G., Integers without large prime factors. J. Théor. Nombres Bordeaux 5(1993), 411–484. http://dx.doi.Org/10.58O2/jtnb.101 Google Scholar
[Hux74] Huxley, M. N., Large values of Dirichlet polynomials (III). Acta Arith. 26(1974), 435–444.Google Scholar
[Jut77] Jutila, M., On Linnik's constant. Math. Scand. 41(1977), 45–62.Google Scholar
[LS12] Lagarias, J. C. et Soundararajan, K., Counting smooth solutions to the equation a + b = c. Proc. London Math. Soc. 104(2012), 770–798.http://dx.doi.Org/10.1112/plms/pdrO37 Google Scholar
[MV06] Montgomery, H. L. et Vaughn, R. C., Multiplicative number theory I: Classical theory. Cambridge Stud. Adv. Math. 97, Cambridge University Press, Cambridge, 2007.Google Scholar
[Ran38] Rankin, R. A., The difference between consecutive prime numbers. J. London Math. Soc. 1(1938), 242–247.http://dx.doi.Org/10.1112/jlms/s1-13.4.242 Google Scholar
[Sai89] Saias, E., Sur le nombre des entiers sans grand facteur premier. J. Number Theory 32(1989), 78–99.http://dx.doi.Org/10.1016/0022-314X(89)90099-1 Google Scholar
[Sou08] Soundararajan, K., The distribution of smooth numbers in arithmetic progressions. In: Anatomy of Integers, CRM Proc. Lecture Notes 46(2008), 115–128.Google Scholar
[Ten90] Tenenbaum, G., Sur un problème d'Erdôs et Alladi. Progr. Math. 91(1990), 221–239.Google Scholar
[TenO8] Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres. Troisième edition. Echelles, Berlin, 2008.Google Scholar