Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dow, A.
and
Peters, T. J.
1988.
Products and remote points: examples and counterexamples.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 4,
p.
1296.
Dow, Alan
1989.
A separable space with no remote points.
Transactions of the American Mathematical Society,
Vol. 312,
Issue. 1,
p.
335.
Hart, Klaas Pieter
and
van Mill, Jan
2016.
Alan Dow.
Topology and its Applications,
Vol. 213,
Issue. ,
p.
2.


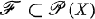
 . We call
. We call