Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T09:30:44.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results Relating the Behaviour of Fourier Transforms Near the Origin and at Infinity

Published online by Cambridge University Press:  20 November 2018

C. Nasim
C. Nasim*
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that under special conditions, Fourier sine transforms and Fourier cosine transforms behave asymptotically like a power of x, either as x → 0 or as x → ∞ or both. For example (3),

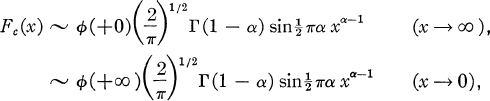
where f(x) = x–αϕ(x), 0 < α < 1, and ϕ(x) is of bounded variation in (0, ∞) and Fc(x) is the Fourier cosine transform of f(x). This suggests that other results connecting the behaviour of a function at infinity with the behaviour of its Fourier or Watson transform near the origin might exist. In this paper wre derive various such results. For example, a special case of these results is

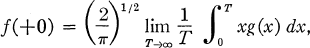
where f(x) is the Fourier sine transform of g(x). It should be noted that the Fourier inversion formula fails to give f(+0) directly in this case. Some applications of these results to show the relationships between various forms of known summation formulae are given.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 942 - 950
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Guinand, A. P., Summation formulae and self-reciprocal functions. II, Quart. J. Math. Oxford Ser. 10 (38) (1939), 104–118.Google Scholar
2. Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford Univ. Press, London, 1948).Google Scholar
3. Watson, G. N., Theory of Bessel functions (Cambridge Univ. Press, New York, 1966).Google Scholar
4. Whittaker, E. T. and Watson, G. N., A course of modern analysis (Cambridge Univ. Press, New York, 1963).Google Scholar