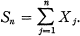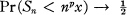Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heyde, C. C.
1967.
On the influence of moments on the rate of convergence to the normal distribution.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 8,
Issue. 1,
p.
12.
Heathcote, C. R.
1967.
Complete exponential convergence and some related topics.
Journal of Applied Probability,
Vol. 4,
Issue. 02,
p.
217.
Heathcote, C. R.
1967.
Complete exponential convergence and some related topics.
Journal of Applied Probability,
Vol. 4,
Issue. 2,
p.
217.
Heyde, C. C.
1967.
Some local limit results in fluctuation theory.
Journal of the Australian Mathematical Society,
Vol. 7,
Issue. 4,
p.
455.
Petrov, V. V.
1970.
On an Estimate of the Concentration Function of a Sum of Independent Random Variables.
Theory of Probability & Its Applications,
Vol. 15,
Issue. 4,
p.
701.
Tsitsiashvili, G. Sh.
1976.
Piecewise-Linear Markov Chains and Analysis of Their Stability.
Theory of Probability & Its Applications,
Vol. 20,
Issue. 2,
p.
337.
Heyde, C. C.
2010.
Selected Works of C.C. Heyde.
p.
63.