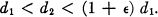Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T00:05:19.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Remarks on Prime Factors of Integers

Published online by Cambridge University Press:  20 November 2018

P. Erdös
P. Erdös*
Affiliation:
University of Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 1 < a1 < a2 < … be a sequence of integers and let N(x) denote the number of a's not exceeding x. If N(x)/x tends to a limit as x tends to infinity we say that the a's have a density. Often one calls it the asymptotic density to distinguish it from the Schnirelmann or arithmetical density. The statement that almost all integers have a certain property will mean that the integers which do not have this property have density 0. Throughout this paper p, q, r will denote primes.

I conjectured for a long time that, if e > 0 is any given number, then almost all integers n have two divisors d1 and d2 satisfying

1

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 11 , 1959 , pp. 161 - 167
Copyright
Copyright © Canadian Mathematical Society 1959

References

1. Erdös, P., On the density of some sequences of integers, Bull. Amer. Math. Soc, 54 (1948), 691.Google Scholar
2. Erdös, P., Some remarks about additive and multiplicative functions, Bull. Amer. Math. Soc, 52 (1946), 533, theorem 9.Google Scholar
3. Erdös, P., On the density of the abundant numbers, J. Lond. Math. Soc, 9 (1934), 279.Google Scholar
4. Hardy, G. H. and Ramanujan, S., The normal number of prime factors of n, Quart. J. Math., 48 (1917), 76–92.Google Scholar
5. Landau, E., Verteilung der Primzahlen,Google Scholar
6. Turán, P., On a theorem of Hardy and Ramanujan, J. Lond. Math. Soc, 9 (1934), 274-6.Google Scholar