Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:30:46.050Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Remarks on IA Automorphisms of Free Groups

Published online by Cambridge University Press:  20 November 2018

J. McCool
J. McCool*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let An be the automorphism group of the free group Fn of rank n, and let Kn be the normal subgroup of An consisting of those elements which induce the identity automorphism in the commutator quotient group 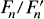. The group Kn has been called the group of IA automorphisms of Fn (see e.g. [1]). It was shown by Magnus [7] using earlier work of Nielsen [11] that Kn is finitely generated, with generating set the automorphisms

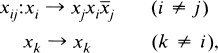
and

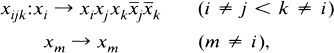
where x1, x2, …, xn, is a chosen basis of Fn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1144 - 1155
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bachmuth, S., Automorphisms of free metabelian groups, Trans. Amer. Math. Soc. 118 (1965), 93–104.Google Scholar
2. Bachmuth, S., Automorphisms of solvable groups, Part 1, Proceedings of Groups — St. Andrews (1985), 1–13 (London Mathematical Society, Lecture Notes Series #121, Cambridge Univ. Press 1986).Google Scholar
3. Bieri, R., Homological dimension of discrete groups, Queen Mary College Mathematics Notes (1976).Google Scholar
4. Chein, O., Subgroups of I A automorphisms of a free group, Acta Mathematica 123 (1969), 1–12.Google Scholar
5. Levinger, B., A generalisation of the braid group, Ph.D. thesis, New York University (1968).Google Scholar
6. Lyndon, R. and Schupp, P. E., Combinatorial group theory (Springer, 1977).Google Scholar
7. Magnus, W., Über n-dimensionale gittertransformationen, Acta Math. 64 (1934), 353–367.Google Scholar
8. McCool, J., A presentation for the automorphism group of a free group of finite rank, J. London Math. Soc. (2) 8 (1974), 259–266.Google Scholar
9. McCool, J., Some finitely presented subgroups of the automorphism group of a free group, J. of Alg. 55(1975), 205–213.Google Scholar
10. McCool, J., On basis-conjugating automorphisms of free groups, Can. J. Math. 38 (1986), 1525–1529.Google Scholar
11. Nielsen, J., Die gruppe der dreidimensionalen Gittertransformationen, Kgl. Danske Videnskabernes Selskeb., Math. Fys. Meddelelser v. 12 (1924), 1–29.Google Scholar