Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:10:49.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Radical Properties of Jordan Matrix Rings

Published online by Cambridge University Press:  20 November 2018

Michael Rich
Michael Rich*
Affiliation:
Temple University, Philadelphia, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a ring (not necessarily associative) in which 2x = a has a unique solution for each a ∈ A. Then it is known that if A contains an identity element 1 and an involution j : x ↦ x and if Ja is the canonical involution on An determined by

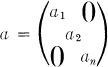
where the ai al−l, 1 ≦ i ≦ n are symmetric elements in the nucleus of A then H(An, Ja), the set of symmetric elements of An, for n ≧ 3 is a Jordan ring if and only if either A is associative or n = 3 and A is an alternative ring whose symmetric elements lie in its nucleus [2, p. 127].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 189 - 196
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Erickson, T. S. and Montgomery, S., The prime radical in special Jordan rings, Trans. Amer. Math. Soc. 156 (1971), 155–164.Google Scholar
2. Jacobson, N., Structure and representations of Jordan algebras, A.M.S. Colloq. Publ. Vol. 39, Providence, 1968.Google Scholar
3. Rich, M., The Levitzki radical in associative and Jordan rings, J. Algebr. 40 (1976), 97–104.Google Scholar
4. Rich, M., On alternative rings with involution, Comm. Algebr. 6 (1978), 1383–1392.Google Scholar