Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T06:25:26.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Properties of Generalized Euler Numbers

Published online by Cambridge University Press:  20 November 2018

D. J. Leeming  and
R. A. Macleod
D. J. Leeming
Affiliation:
University of Victoria, Victoria, British Columbia
R. A. Macleod
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define infinitely many sequences of integers 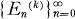one sequence for each positive integer k ≦ 2 by

(1.1)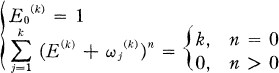

where 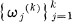are the k-th roots of unity and (E(k))n is replaced by En(k) after multiplying out. An immediate consequence of (1.1) is

(1.2)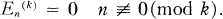

Therefore, we are interested in numbers of the form Esk(k) (s = 0, 1, 2, …; k = 2, 3, …).

Some special cases have been considered in the literature. For k = 2, we obtain the Euler numbers (see e.g. [8]). The case k = 3 is considered briefly by D. H. Lehmer [7], and the case k = 4 by Leeming [6] and Carlitz ([1]and [2]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 606 - 617
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Carlitz, L., Some arithmetic properties of a special sequence of integers, Can. Math. Bull. 19 (1976), 425–429.Google Scholar
2. Carlitz, L., Combinatorial property of a special polynomial sequence, Can. Math. Bull. 20 (1977), 183–188.Google Scholar
3. Carlitz, L., Permutations with prescribed pattern, Math. Nach. 58 (1973), 31–53.Google Scholar
4. Frobenius, F. G., Uber die Bernoulli schen Zahlen und die Eulerschen Polynôme, Gesammelte Abhandlungen III (Springer, Berlin-Heidelberg-New York, 1968), 440–478.Google Scholar
5. Gould, H. W., Combinatorial identities (Morgantown Printing and Binding Co., 1972).Google Scholar
6. Leeming, D. J., Some properties of a certain set of interpolating polynomials, Can. Math. Bull. 18 (1975), 529–537.Google Scholar
7. Lehmer, D. H., Lacunar y recurrence formulas for the numbers of Bernoulli and Euler, Ann. Math. 36 (1935), 637–649.Google Scholar
8. Norlund, N. E., Mémoire sur les polynômes de Bernoulli, Acta Math. 23 (1920), 121–144.Google Scholar