Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-25T20:51:47.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Problems for Typically Real Functions

Published online by Cambridge University Press:  20 November 2018

James A. Jenkins
James A. Jenkins*
Affiliation:
Washington University, St. Louis
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Many extremal properties of the class of normalized univalent functions are shared by the class of typically real functions each considered in the unit circle. By the class T of typically real functions we mean those functions f(z), regular for |z| < 1 with f(0) = 0, f'(0) = 1, and such that 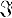f(z) > 0 for 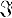z > 0, 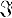(z) < 0 for 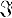> 0. This class was first studied by Rogosinski (4) who proved various simple properties for it. Later Robertson (3) took up the study and proved the following important representation result.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 299 - 304
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Gronwall, T. H., On the distortion in conformai mapping when the second coefficient in the mapping function has an assigned value, Proc. Nat. Acad. Sci. U.S.A., 6 (1920), 300–302.Google Scholar
2. Jenkins, James A., On a problem of Gronwall, Ann. Math., 59 (1954), 490–504.Google Scholar
3. Robertson, M. S., On the coefficients of a typically-real function, Bull. Amer. Math. Soc, 41 (1935), 565–572.Google Scholar
4. Rogosinski, W., Ueber positive harmonische Entwicklungen und typisch-reelle Potenzreihe, Math. Zeit, 35 (1932), 93–121.Google Scholar
5. Widder, D. V., The Laplace transform (Princeton University Press, 1946).Google Scholar