Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T15:58:22.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Norms on Universal Enveloping Algebras

Published online by Cambridge University Press:  20 November 2018

Leonard Gross
Leonard Gross*
Affiliation:
Department of Mathematics Cornell University Ithaca, New York 14853 U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The universal enveloping algebra, 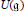$U(\mathfrak{g})$, of a Lie algebra $\mathfrak{g}$ supports some norms and seminorms that have arisen naturally in the context of heat kernel analysis on Lie groups. These norms and seminorms are investigated here from an algebraic viewpoint. It is shown that the norms corresponding to heat kernels on the associated Lie groups decompose as product norms under the natural isomorphism 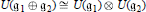$U({{\mathfrak{g}}_{1\,}}\oplus \,{{\mathfrak{g}}_{2}})\,\cong \,U({{\mathfrak{g}}_{1}})\,\otimes \,U({{\mathfrak{g}}_{2}})$. The seminorms corresponding to Green's functions are examined at a purely Lie algebra level for 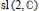$\text{sl(2,}\,\mathbb{C}\text{)}$. It is also shown that the algebraic dual space 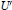${U}'$ is spanned by its finite rank elements if and only if $\mathfrak{g}$ is nilpotent.

Keywords

17B3516S3022E30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 2 , 01 April 1998 , pp. 356 - 377
Copyright
Copyright © Canadian Mathematical Society 1998

References

[BSZ] Baez, John C., Segal, Irving E., and Zhou, Zhengfang, Introduction to Algebraic and Constructive Quantum Field Theory. Princeton Univ, Press, Princeton, New Jersey, 1992.Google Scholar
[B] Bourbaki, N., Lie groups and Lie algebras. Chapters I–III, Springer-Verlag, New York, 1989.Google Scholar
[Co] Cook, J., The mathematics of second quantization. Trans. Amer. Math. Soc. 74(1953), 222–245.Google Scholar
[D] Driver, B.K., On the Kakutani-Itô-Segal-Gross and the Segal-Bargmann-Hall isomorphisms. J. Funct. Anal. 133(1995), 69–128.Google Scholar
[DG] Driver, B.K. and Gross, L., Hilbert spaces of holomorphic functions on complex Lie groups. In: New Trends in Stochastic Analysis, Proceedings of the 1994 Taniguchi Symposium (Eds. Elworthy, K., Kusuoka, S. and Shigekawa, I.),World Scientific, 1997. 76–106.Google Scholar
[Di] Dixmier, J., Enveloping Algebras. North-Holland Publ. Co., Amsterdam, New York, Oxford, 1977.Google Scholar
[G1] Gross, L., Uniqueness of ground states for Schrödinger operators over loop groups. J. Funct. Anal. 112(1993), 373–441.Google Scholar
[G2] Gross, L., The homogeneous chaos over compact Lie groups. In: Stochastic Processes, A Festschrift in Honor of Gopinath Kallianpur, (eds. Cambanis, S., et al.), Springer-Verlag, New York, 1993. 117–123.Google Scholar
[G3] Gross, L., Harmonic analysis for the heat kernel measure on compact homogeneous spaces. In: Stochastic Analysis on Infinite Dimensional Spaces,Kunita and Kuo, Longman House, Essex, England, 1994. 99–110.Google Scholar
[G4] Gross, L., A local Peter-Weyl theorem. Trans. Amer. Math. Soc., to appear.Google Scholar
[GM] Gross, L. and Malliavin, P., Hall's transform and the Segal-Bargmann map. In: Ito's Stochastic Calculus and Probability Theory, (eds. Ikeda, Watanabe, Fukushima, Kunita), Springer-Verlag, Tokyo, Berlin, New York, 1996. 73–116.Google Scholar
[Ha1] Hall, B., The Segal-Bargmann “coherent state” transform for compact Lie groups. J. Funct. Anal. 122(1994), 103–151.Google Scholar
[Ha2] Hall, B., The inverse Segal-Bargmann transform for compact Lie groups. J. Funct. Anal. 143(1997), 98–116.Google Scholar
[Ha3] Hall, B., Personal communication. November, 1996.Google Scholar
[Hij1] Hijab, Omar, Hermite functions on compact Lie groups I. J. Funct. Anal. 125(1994), 480–492.Google Scholar
[Hij2] Hijab, Omar, Hermite functions on compact Lie groups II. J. Funct. Anal. 133(1995), 41–49.Google Scholar
[K] Klauder, John R., Exponential Hilbert space: Fock space revisited. J. Math. Phys. 11(1969), 609–630.Google Scholar
[P] Parthasarathy, K.R., An introduction to quantum stochastic calculus. Birkhäuser Verlag, Basel, Boston, Berlin, 1992.Google Scholar
[R] Ree, Rimhak, Lie elements and an algebra associated with shuffles. Ann. of Math. 68(1958), 210–220.Google Scholar
[So] Solomon, Louis, On the Poincaré-Birkhoff-Witt theorem. J. Combin. Theory 4(1968), 363–375.Google Scholar
[Sw] Sweedler, Moss, Hopf Algebras. W. A. Benjamin, Inc., New York, 1969.Google Scholar
[V] Varadarajan, V.S., Lie groups, Lie algebras, and their representations. Springer-Verlag, New York, 1984.Google Scholar