Published online by Cambridge University Press: 04 November 2020
In this work, we obtain a local maximum principle along the Ricci flow 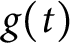 $g(t)$
under the condition that
$g(t)$
under the condition that
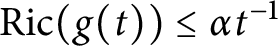 $\mathrm {Ric}(g(t))\le {\alpha } t^{-1}$
for
$\mathrm {Ric}(g(t))\le {\alpha } t^{-1}$
for
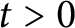 $t>0$
for some constant
$t>0$
for some constant
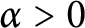 ${\alpha }>0$
. As an application, we will prove that under this condition, various kinds of curvatures will still be nonnegative for
${\alpha }>0$
. As an application, we will prove that under this condition, various kinds of curvatures will still be nonnegative for
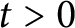 $t>0$
, provided they are non-negative initially. These extend the corresponding known results for Ricci flows on compact manifolds or on complete noncompact manifolds with bounded curvature. By combining the above maximum principle with the Dirichlet heat kernel estimates, we also give a more direct proof of Hochard’s [15] localized version of a maximum principle by Bamler et al. [1] on the lower bound of different kinds of curvatures along the Ricci flows for
$t>0$
, provided they are non-negative initially. These extend the corresponding known results for Ricci flows on compact manifolds or on complete noncompact manifolds with bounded curvature. By combining the above maximum principle with the Dirichlet heat kernel estimates, we also give a more direct proof of Hochard’s [15] localized version of a maximum principle by Bamler et al. [1] on the lower bound of different kinds of curvatures along the Ricci flows for
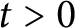 $t>0$
.
$t>0$
.
Research partially supported by NSF grant DMS-1709894. Research partially supported by Hong Kong RGC General Research Fund #CUHK 14301517.