Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T20:09:18.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Finiteness Conditions for Orthomodular Lattices

Published online by Cambridge University Press:  20 November 2018

Günter Bruns  and
Richard Greechie
Günter Bruns
Affiliation:
McMaster University, Hamilton, Ontario
Richard Greechie
Affiliation:
Kansas State University, Manhattan, Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper L will be an orthomodular lattice and 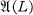the set of all maximal Boolean subalgebras, also called blocks [4], of L. For every x ∈ L, C(x) will be the set of all elements of L which commute with x. Let n ≧ 1 be a natural number. In this paper we consider the following conditions for L:

An: L has at most n blocks,

Bn: there exists a covering of L by at most n blocks,

Cn: the set ﹛C(x)| x ∈ L﹜ has at most n elements,

Dn: out of any n + 1 elements of L at least two commute.

We also consider quantified versions of these statements, namely the statements A, B, C, D defined by: A ⇔ ∃ nAn, B ⇔ ∃ nBn, C ⇔ ∃ nCn and D ⇔ ∃ nDn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 535 - 549
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Bruns, G., A finiteness criterion for orthomodular lattices. Can. J. Math. 30 (1978), 315–320.Google Scholar
2. Bruns, G., Block-finite orthomodular lattices, Can. J. Math. 31 (1979), 961–985.Google Scholar
3. Foulis, D. J., A note on orthomodular lattices, Portugal Math. 21 (1962), 65–72.Google Scholar
4. Greechie, R. J., On the structure of orthomodular lattices satisfying the chain condition, J. Combinatorial Theory 4 (1968), 210–218.Google Scholar
5. Holland, S. S., A Radon-Nikodym theorem for dimension lattices, Trans. AMS 108 (1963), 66–87.Google Scholar