Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T08:46:22.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Examples of Normal Moore Spaces

Published online by Cambridge University Press:  20 November 2018

Mary Ellen Rudin  and
Michael Starbird
Mary Ellen Rudin
Affiliation:
University of Wisconsin, Madison, Wisconsin
Michael Starbird
Affiliation:
University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A normal Moore space is non-metrizable only if it fails to be ƛ-collectionwise normal for some uncountable cardinal ƛ [1].

For each uncountable cardinal X we present a class 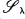of normal, locally metrizable Moore spaces and a particular space Sλ in 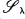. If there is any space of class 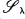which is not X-collectionwise normal, then Sλ is such a space. The conditions for membership in 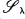make a space in 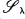behave like a subset of a product of a Moore space with a metric space. The class 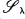is sufficiently large to allow us to prove the following. Suppose F is a locally compact, 0-dimensional Moore space (not necessarily normal) with a basis of cardinality X and M is a metric space which is O-dimensional in the covering sense. If there is a normal, not X-collectionwise normal Moore space X where X ⊂ Y × M, then Sx is a normal, not λ-collectionwise normal Moore space.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 1 , 01 February 1977 , pp. 84 - 92
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Bing, R. H., Metrization of topological spaces, Can. J. Math. 3 (1951), 175–186.Google Scholar
2. Fleissner, W., When normal implies collectionwise Hausdorff: consistency results, Thesis, University of California, Berkeley 1974.Google Scholar
3. Tall, F., Set-theoretic consistency results and topological theorems concerning the normal Moore space conjecture and related problems, Thesis, University of Wisconsin, Madison 1969.Google Scholar