No CrossRef data available.
 Division Algebras
Division AlgebrasPublished online by Cambridge University Press: 20 November 2018
Let K* be an associative algebra over a field F with identity u, and let u, e1, e2, … , be a basis for K*. Denote by K the linear space, over F, spanned by the ei,i = 1, 2, … . Then for x, y in K, xy = αu + a, where a ∈ K. Define h(x, y) = α and x.y = a. With respect to the operation thus defined, K becomes an algebra over F satisfying
1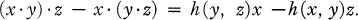
Further, the bilinear form h(x, y) is associative on K. Any algebra, over a field F, which possesses an associative bilinear form h(x, y) and satisfies (1) will be called a  algebra. It is not difficult to show that any
algebra. It is not difficult to show that any  algebra K can be obtained from a unique associative algebra K* with identity by the process described above. The algebra K* will be called the associated associative algebra of K.
algebra K can be obtained from a unique associative algebra K* with identity by the process described above. The algebra K* will be called the associated associative algebra of K.