Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-13T08:12:09.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Convexity Features Associated with Unitary Orbits

Published online by Cambridge University Press:  20 November 2018

Man-Duen Choi ,
Chi-Kwong Li  and
Yiu-Tung Poon
Man-Duen Choi
Affiliation:
Department of Mathematics, University of Toronto Toronto, Ontario, M5S 3G3, e-mail: [email protected]
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William & Mary, Williamsburg, Virginia 23187, U.S.A., e-mail: [email protected]
Yiu-Tung Poon
Affiliation:
Department of Mathematics, Iowa State University, Ames, Iowa 50011, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 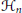${{\mathcal{H}}_{n}}$ be the real linear space of 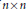$n\,\times \,n$ complex Hermitian matrices. The unitary (similarity) orbit 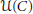$\mathcal{U}\left( C \right)$ of 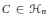$C\,\in \,{{\mathcal{H}}_{n}}$ is the collection of all matrices unitarily similar to 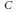$C$. We characterize those 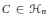$C\,\in \,{{\mathcal{H}}_{n}}$ such that every matrix in the convex hull of 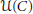$\mathcal{U}\left( C \right)$ can be written as the average of two matrices in 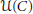$\mathcal{U}\left( C \right)$. The result is used to study spectral properties of submatrices of matrices in 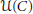$\mathcal{U}\left( C \right)$, the convexity of images of 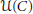$\mathcal{U}\left( C \right)$ under linear transformations, and some related questions concerning the joint 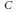$C$-numerical range of Hermitian matrices. Analogous results on real symmetric matrices are also discussed.

Keywords

15A6015A42Hermitian matrixunitary orbiteigenvaluejoint numerical range
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 91 - 111
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Au-Yeung, Y. H. and Tsing, N. K., An extension of the Hausdorff-Toeplitz theorem on the numerical range. Proc. Amer. Math. Soc. 89 (1983), 215–218.Google Scholar
[2] Azenhas, O., The admissible interval for the invariant factors of a product of matrices. 1998, preprint.Google Scholar
[3] Bhatia, R., Choi, M. D. and Davis, C., Comparing a matrix to its off-diagonal part. Oper. Theory Adv. Appl. 40 (1989), 151–164.Google Scholar
[4] Bebiano, N., Li, C. K. and da Providencia, J., Product of diagonal elements of matrices. Linear Algebra Appl. 178 (1993), 185–200.Google Scholar
[5] Binding, P., Farenick, D. and Li, C. K., A dilation and norm in several variable operator theory. Canad. J. Math. 47 (1995), 449–461.Google Scholar
[6] Binding, P. and Li, C. K., Joint ranges of Hermitian matrices and simultaneous diagonalization. Linear Algebra Appl. 151 (1991), 157–168.Google Scholar
[7] Buch, A. S., The saturation conjecture (after A. Knutson and T.Tao). Enseign. Math. (2) 46 (2000), 43–60.Google Scholar
[8] Cho, M. and Takaguchi, M., Some classes of commuting m-tuples of operators. Studia Math. 80 (1984), 245–259.Google Scholar
[9] Choi, M. D. and Wu, P. Y., Convex combinations of projections. Linear Algebra Appl. 136 (1990), 25–42.Google Scholar
[10] Doyle, J. C., Analysis of feedback systems with structured uncertainties. Proc. IEEE-D (6) 129 (1982), 242–250.Google Scholar
[11] Day, J., So, W. and Thompson, R. C., The spectrum of a Hermitian matrix sum. Linear Algebra Appl. 280 (1998), 289–332.Google Scholar
[12] Fan, K. and Pall, G., Imbedding conditions for Hermitian and normal matrices. Canad. J. Math. 9 (1957), 298–304.Google Scholar
[13] Fan, M. and Tits, A., m-form numerical range and the computation of the structured singular values. IEEE Trans. Automat. Control 33 (1988), 284–289.Google Scholar
[14] Fulton, W., Eigenvalues of sums of Hermitian matrices (after A. Klyachko). Séminaire Bourbaki 845, June 1998, Astérisque 252 (1998), 255–269.Google Scholar
[15] Goldberg, M. and Straus, E. G., Elementary inclusion relations for generalized numerical ranges. Linear Algebra Appl. 18 (1977), 1–24.Google Scholar
[16] Helmke, U. and Rosenthal, J., Eigenvalue inequalities and Schubert calculus.Math. Nachr. 171 (1995), 207–225.Google Scholar
[17] Horn, A., Doubly Stochastic matrices and the diagonal of a rotation matrix. Amer. J. Math. 76 (1954), 620–630.Google Scholar
[18] Horn, A., Eigenvalues of sums of Hermitian matrices. Pacific J. Math. 12 (1962), 225–241.Google Scholar
[19] Horn, R. A. and Johnson, C. R.. Topics in Matrix Analysis. Cambridge University Press, 1991.Google Scholar
[20] Klyachko, A. A., Stable bundles, representation theory and Hermitian operators. Selecta Math. (N.S.) 4 (1998), 419–445.Google Scholar
[21] Knutson, A. and Tao, T., The honeycomb model of the Berenstein-Zelevinsky polytope I: Klyacho's saturation conjecture. lanl preprint, 1998.Google Scholar
[22] Li, C. K., Matrices with some extremal properties. Linear Algebra Appl. 101 (1988), 255–267.Google Scholar
[23] Li, C. K. and Mathias, R., Inequalities on the singular values of an off-diagonal block of a Hermitian matrix. J. Inequal. Appl. 3 (1999), 137–142.Google Scholar
[24] Li, C. K. and Poon, Y. T., Convexity of the k-th joint numerical range. SIAM J. Matrix Analysis Appl. 21 (1999), 668–678.Google Scholar
[25] Li, C. K. and Poon, Y. T., Off diagonal submatrices of a Hermitian matrix. Submitted; preprint available at http://www.resnet.wm.edu/.cklixx/poon-9.pdf. Google Scholar
[26] Li, C. K. and Tam, T. Y., Numerical ranges arising from simple Lie algebras. Canad. J. Math. 52 (2000), 141–171.Google Scholar
[27] Li, C. K. and Tsing, N. K., On the k-th matrix numerical range. Linear and Multilinear Algebra 28 (1991), 229–239.Google Scholar
[28] Marshall, A. W. and Olkin, I., Inequalities: The Theory of Majorizations and Its Applications. Academic Press, 1979.Google Scholar
[29] Mirsky, L., Matrices with prescribed characteristic roots and diagonal elements. J. LondonMath. Soc. 33 (1958), 14–21.Google Scholar
[30] Poon, Y. T., Another proof of a result of Westwick. Linear and Multilinear Algebra 9 (1980), 181–186.Google Scholar
[31] Poon, Y. T., On the convex hull of the multiform numerical range. Linear and Multilinear Algebra 37 (1994), 221–224.Google Scholar
[32] Schur, I., Über eine Klasse von Mittelbildungen mit Anwendungen die Determinanten-Theorie Sitzungsber. Berlin.Math. Gesellschaft 22(1923), 9–20, see also, Issai Schur Collected Works. (eds. A. Brauer and H. Rohrbach), Vol. II. 416–427. Springer-Verlag, Berlin, 1973.Google Scholar
[33] Tam, B. S., A simple proof of Goldberg-Straus theorem on numerical radii. Glasgow Math. J. 28 (1986), 139–141.Google Scholar
[34] Thompson, R. C., Singular values, diagonal elements, and convexity. SIAM J. Appl. Math. 32 (1977), 39–63.Google Scholar
[35] Thompson, R. C., Research problem: The matrix numerical range. Linear and Multilinear Algebra 21 (1987), 321–323.Google Scholar
[36] Warner, F. W., Foundations of Differentiable Manifolds and Lie Groups. Scott. Foresman, London, 1971.Google Scholar
[37] Westwick, R., A theorem on numerical ranges. Linear and Multilinear Algebra 2 (1975), 311–315.Google Scholar
[38] Zelevinsky, A., Littlewood-Richardson semigroups. MSRI, 1997-044, preprintGoogle Scholar