In this paper we construct two examples which elucidate the relationships between several σ-algebras that arise in measure-theoretic constructions on locally compact spaces and groups. For any space X let 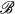(X) be the Borelσ-algebra on X, i.e., the smallest σ-algebra of subsets of X which contains the family of all closed subsets of X. Let δ (X) be the smallest δ-ring of subsets of X which contains every compact subset of X, where by a δ-ring we mean a collection of subsets of X which is closed under the formation of countable intersections, finite unions and relative complements. Let σ(X) be the smallest σ-ring of subsets of X which contains all compact subsets of X, where by a σ-ring we mean a collection of subsets of X which is closed under the formation of countable unions, finite intersections and relative complements.