Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T12:11:16.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Applications of Artamonov-Quillen-Suslin Theorems to Metabelian Inner Rank and Primitivity

Published online by Cambridge University Press:  20 November 2018

C. K. Gupta ,
N. D. Gupta  and
G. A. Noskov
C. K. Gupta
Affiliation:
University of Manitoba Winnipeg, Manitoba R3T2N2 e-mail:[email protected]
N. D. Gupta
Affiliation:
University of Manitoba Winnipeg, Manitoba R3T2N2 e-mail:[email protected]
G. A. Noskov
Affiliation:
Institute of Information Technology and Applied Mathematics Omsk 644 Russia e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any variety 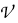of groups, the relative inner rank of a given groupG is defined to be the maximal rank of the 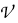-free homomorphic images of G. In this paper we explore metabelian inner ranks of certain one-relator groups. Using the well-known Quillen-Suslin Theorem, in conjunction with an elegant result of Artamonov, we prove that if r is any "Δ-modular" element of the free metabelian group Mn of rank n > 2 then the metabelian inner rank of the quotient group Mn/(r) is at most [n/2]. As a corollary we deduce that the metabelian inner rank of the (orientable) surface group of genus k is precisely k. This extends the corresponding result of Zieschang about the absolute inner ranks of these surface groups. In continuation of some further applications of the Quillen-Suslin Theorem we give necessary and sufficient conditions for a system g = (g1,..., gk) of k elements of a free metabelian group Mn, k ≤ n, to be a part of a basis of Mn. This extends results of Bachmuth and Timoshenko who considered the cases k = n and k < n — 3 respectively.

Keywords

20F9920F0520H25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 2 , 01 April 1994 , pp. 298 - 307
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Artamonov, V. A., Projective metabelian groups and Lie Algebras, Izv. Akad. Nauk SSSR Sen Mat. 42 (1978), 226–236.Google Scholar
2. Artamonov, V. A., The categories of free metabelian groups and Lie algebras, Comment. Math. Univ. Carolin. 18(1977), 143–159.Google Scholar
3. Bachmuth, S., Automorphisms of free metabelian groups, Trans. Amer. Math. Soc. 118(1965), 93–104.Google Scholar
4. Baumslag, Gilbert and Steinberg, Arthur, Residual nilpotence and relations in free groups, Bull. Amer. Math. Soc. 70(1964), 283–284.Google Scholar
5. Buchsbaum, David A. and Eisenbud, David, What makes a complex exact?, J. Algebra 25(1973), 259–268.Google Scholar
6. Groves, J. R. J. and Miller, Charles F., III, Recognizing free metabelian groups, Illinois J. Math. 30(1986), 246–254.Google Scholar
7. Gupta, Narain, Free Group Rings, Amer. Math. Soc., Contemporary Math. 66(1987).Google Scholar
8. Jaco, William, Geometric realizations for free quotients, J. Austral. Math. Soc. 14(1972), 411–418.Google Scholar
9. Linnell, P. A., Mclsaac, A. J. and Webb, P. J., Bounding the number of generators of a metabelian group, Arch. Math. 38(1982), 501–505.Google Scholar
10. Lyndon, R. C., Products of powers in groups, Comm. Pure Appl. Math. 26(1973), 781–784.Google Scholar
11. Lyndon, Roger C. and Schupp, Paul E., Combinatorial Group Theory, Ergeb. der Math. u. ihrer Grenz. 89, Springer-Verlag, New York, 1977.Google Scholar
12. Noskov, G. A., On genus of a free metabelian group, Novosibirsk (509), Vychislitelny Centre of Akad. Nauk. USSR, 1984, preprint.Google Scholar
13. Quillen, Daniel, Projective modules over polynomial rings, Invent. Math. 36(1976), 167–171.Google Scholar
14. Roman'kov, V. A., Criteria for the primitivity of a system of elements of a free metabelian group, Ukrain. Mat. Zh. 43(1991),996-1002.Google Scholar
15. Stallings, John R., Quotients of the powers of the augmentation ideal in a group ring. In: Annals of Math. Study 84(1975), 101–118.Google Scholar
16. Steinberg, Arthur, On free nilpotent quotient groups, Math. Z. 85(1964), 185–196.Google Scholar
17 Steinberg, Arthur, On equations in free groups, Michigan Math. J. 18(1971), 87–95.Google Scholar
18. Suslin, A. A., Projective modules over polynomial rings are free, Dokl. Akad. Nauk SSSR 229(1976), 1063–1066.Google Scholar
19. Suslin, A. A., On the structure of a special linear group over polynomial rings, Izv. Akad. Nauk SSSR Ser. Mat. 41(1977), 235–252.Google Scholar
20. Swan, Richard G., Projective modules over Laurent polynomial rings, Trans. Amer. Math. Soc. 237(1978), 111–120.Google Scholar
21. Timoshenko, E. I., Certain algorithmic questions for metabelian groups, Algebra and Logic 12( 1973), 132- 137; Russian edition: Algebra i Logika 12(1973), 232–240.Google Scholar
22. Timoshenko, E. I., On embedding of given elements into a basis of free metabelian groups, Russian, preprint.Google Scholar
23. Zieschang, H., Über einfache Kurven aufvollbrezeln, Abh. Math. Sem. Univ. Hamburg 25(1962), 231-250.Google Scholar