Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:04:33.338Z Has data issue: false hasContentIssue false
  • English
  • Français

Solving Linear Operator Equations

Published online by Cambridge University Press:  20 November 2018

Chandler Davis  and
Peter Rosenthal
Chandler Davis
Affiliation:
University of Toronto, Toronto, Ontario
Peter Rosenthal
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

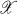Let be a complex Banach space and 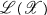the algebra of bounded operators on 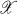. M. Rosenblum's theorem [13; 12] (also discovered by M. G. Kreĭn, cf. [9]) states that (if A, B are fixed bounded operators) the spectrum of the operator 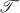on 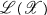defined by 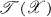= AX – XB is contained in σ (A) – σ(B) = {α – β : α∊σ(A), β∊σ(B)}. In particular, the condition σ(A) ∩ σ(B) = Ø implies that for each Y ∊ 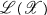there is a unique X ∊ 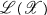such that AX – XB = Y. This does not completely settle the question of solvability of the equation AX – XB = Y: for example, if A is the backward unilateral shift and B = 0, then the equation has a solution (for any Y) even though σ(B) ⊆ σ(A).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1384 - 1389
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Banach, S., Théorie des opérations linéaires (Monografje Matematyczne, Warsaw, 1932).Google Scholar
2. Berberian, S. K., Approximate proper vectors, Proc. Amer. Math. Soc. 13 (1962), 111–114.Google Scholar
3. Calkin, J. W., Two-sided ideals and congruences in the ring of bounded operators in Hilbert space, Ann. of Math. 42 (1941), 839–873.Google Scholar
4. Choi, M. D. and Davis, Ch., The spectral mapping theorem for joint approximate point spectrum, Bull. Amer. Math. Soc. 80 (1974), 317–321.Google Scholar
5. Gohberg, I. C. and Krupnik, N. Ja., Introduction to the theory of one-dimensional singular integral operators (Izdat. Stiinca, Kishinev, 1973). (In Russian.) 6. R. Harte, Spectral mapping theorems on a tensor product, Bull. Amer. Math. Soc. 79 (1973), 367–372.Google Scholar
7. Gohberg, I. C. and Krupnik, N. Ja., Tensor products, multiplication operators and the spectral mapping theorem, Proc. Roy. Irish Acad. Sec. A (to appear).Google Scholar
8. Hirschfeld, R. A., On hulls of linear operators, Math. Z. 96 (1967), 216–222.Google Scholar
9. Kreĭn, M. G., Some new studies of perturbation theory of self-adjoint operators, First Mathematical Summer School (Naukova Dumka, Kiev, 1964). (In Russian.) 10. J. Lindenstrauss and L. Tzafriri, On the complemented subspaces problem, Israel J. Math. 9 (1971), 263–269.Google Scholar
11. Lindenstrauss, J. and H. Rosenthal, Automorphisms in C0, l1, m, Israel J. Math. 7 (1969), 227–239.Google Scholar
12. Lumer, G. and Rosenblum, M., Linear operator equations, Proc. Amer. Math. Soc. 10 (1959), 32–41.Google Scholar
13. Rosenblum, M., On the operator equation BX - XA = Q, Duke Math. J. 23 (1956), 263–269.Google Scholar
14. Taylor, A. E., Introduction to functional analysis (Wiley, New York, 1958).Google Scholar