Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T18:28:38.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Solutions for Semilinear Elliptic Systems with Critical Sobolev Exponent and Hardy Potential

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  20 November 2018

Mohammed Bouchekif  and
Yasmina Nasri
Mohammed Bouchekif
Affiliation:
Université de Tlemcen, Faculté des sciences, Département de mathématiques, BP 119 Tlemcen 13000, Algérie, e-mail: [email protected], [email protected]
Yasmina Nasri
Affiliation:
Université de Tlemcen, Faculté des sciences, Département de mathématiques, BP 119 Tlemcen 13000, Algérie, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider an elliptic system with an inverse square potential and critical Sobolev exponent in a bounded domain of 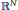${{\mathbb{R}}^{N}}$. By variational methods we study the existence results.

Keywords

critical Sobolev exponentPalais–Smale conditionLinking theoremHardy potential

MSC classification

Secondary: 35B25: Singular perturbations 35B33: Critical exponents 35J50: Variational methods for elliptic systems 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 19 - 33
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] C. O., Alves, D. C., de Morais Filho and M. A., S. Souto, On systems of elliptic equations involving subcritical or critical Sobolev exponents. Nonlinear Anal. 42(2000), 771-787. doi:10.1016/S0362-546X(99)00121-2Google Scholar
[2] A., Ambrosetti and P. H., Rabinowitz, Dual variational methods in critical point theory and applications. J. Funct. Anal. 14(1973), 349-381. doi:10.1016/0022-1236(73)90051-7Google Scholar
[3] Brézis, H. and E., Lieb, A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer.Math. Soc. 88(1983), 486-490. doi:10.2307/2044999Google Scholar
[4] Brézis, H. and L., Nirenberg, Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm. Pure Appl. Math. 36(1983), 437-477. doi:10.1002/cpa.3160360405Google Scholar
[5] A., Cappozi, D., Fortunato and G., Palmieri, An existence result for nonlinear elliptic problems involving critical Sobolev exponent. Ann. Inst. H. Poincaré Anal. Non Linéaire 2(1985), 463-470.Google Scholar
[6] D., Cao and P., Han, Solutions for semilinear elliptic equations with critical exponents and Hardy potential. J. Differential Equations 205(2004), 521-537. doi:10.1016/j.jde.2004.03.005Google Scholar
[7] J., Chen, Existence of solutions for a nonlinear PDE with an inverse square potential. J. Differential Equations 195(2003), 497-519. doi:10.1016/S0022-0396(03)00093-7Google Scholar
[8] D. G., de Figueiredo, Semilinear elliptic systems. In: Lecture Notes at the Second School on Nonlinear Functional Analysis and Applications to Differential Equations at ICTP of Trieste (April 21-May 9, 1997).Google Scholar
[9] A., Ferrero and F., Gazzola, Existence of solutions for singular critical growth semilinear elliptic equations. J. Differential Equations 177(2001), 494-522. doi:10.1006/jdeq.2000.3999Google Scholar
[10] N., Ghoussoub and C., Yuan, Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents. Trans. Amer.Math. Soc. 352(2000), 5703-5743. doi:10.1090/S0002-9947-00-02560-5Google Scholar
[11] E., Jannelli, The role played by space dimension in elliptic critical problems. J. Differential Equations 156(1999), 407-426. doi:10.1006/jdeq.1998.3589Google Scholar
[12] S., Terracini, On positive solutions to a class equations with singular coefficient and critical exponent. Adv. Differential Equations 1(1996), 241-264.Google Scholar