Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-13T08:27:40.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Solution Space Decompositions for nth Order Linear Differential Equations

Published online by Cambridge University Press:  20 November 2018

G. B. Gustafson  and
S. Sedziwy
G. B. Gustafson
Affiliation:
University of Utah, Salt Lake City, Utah
S. Sedziwy
Affiliation:
University of Utah, Salt Lake City, Utah
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the wth order scalar ordinary differential equation

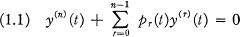
with pr ∈ C([0, ∞) → R ) . The purpose of this paper is to establish the following:

DECOMPOSITION THEOREM. The solution space X of (1.1) has a direct sum Decomposition

where M1 and M2 are subspaces of X such that

(1) each solution in M1\﹛0﹜ is nonzero for sufficiently large t ﹛nono sdilatory) ;

(2) each solution in M2 has infinitely many zeros ﹛oscillatory).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 3 , 01 June 1975 , pp. 508 - 512
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Dolan, J. M., On the relationship between a linear third order equation and its adjoint, J. Differential Equations 7 (1970), 367–388.Google Scholar
2. Dolan, J. M. and Klaasen, G. A., Strongly oscillatory and nonoscillatory subspaces of linear equations, Can. J. Math. 27 (1975), 106–110.Google Scholar
3. Dunford, N. and Schwartz, J. T., Linear operators, part I: general theory (Interscience, New York, 1958).Google Scholar
4. Gustafson, G. B., Higher order separation and comparison theorems, with applications to solution space problems, Ann. Mat. Pura Appl. 95 (1973), 245–254.Google Scholar
5. Gustafson, G. B., The nonequivalence of oscillation and nondisconjugacy, Proc. Amer. Math. Soc. 25 (1970), 254–260.Google Scholar
6. Neuman, F., On two problems on oscillations of linear differential equations of the third order, preprint (Brno, Czechoslovakia), to appear.Google Scholar
7. Krasnoselskii, M. A., Positive solutions of operator equations (P. Noordhoof Ltd., Groningen, The Netherlands, 1964).Google Scholar