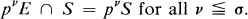Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:06:39.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Solution of a Problem of L. Fuchs Concerning Finite Intersections of Pure Subgroups

Published online by Cambridge University Press:  20 November 2018

R. Göbel  and
R. Vergohsen
R. Göbel
Affiliation:
Universität Essen, Essen, West Germany
R. Vergohsen
Affiliation:
Universität Essen, Essen, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

L. Fuchs states in his book “Infinite Abelian Groups” [6, Vol. I, p. 134] the following

Problem 13. Find conditions on a subgroup of A to be the intersection of a finite number of pure (p-pure) subgroups of A.

The answer to this problem will be given as a special case of our theorem below. In order to find a better setting of this problem recall that a subgroup S ⊆ E is p-pure if pnE ∩ S = pnS for all natural numbers. Then S is pure in E if S is p-pure for all primes p. This generalizes to pσ-isotype, a definition due to L. J. Kulikov, cf. [6, Vol. II, p. 75] and [11, pp. 61, 62]. If α is an ordinal, then S is pσ-isotype if

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 304 - 327
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Becv´r, J., Intersections of Γ-isotype subgroups in abelian groups, Proc. Amer. Math. Soc. 56 (1982), 199–204.Google Scholar
2. Benabdallah, K. and Robert, S., Intersections finies des sous-groupes nets, Can. J. Math. 32 (1980), 885–892.Google Scholar
3. Boyer, D. and Rangaswamy, K. M., Intersections of pure subgroups in abelian groups, Proc. Amer. Math. Soc. 81 (1981), 178–180.Google Scholar
4. Charles, B., Une caractérisation des intersections de sousgroupes divisibles, C.R. Acad. Sci. Paris 250 (1960), 256–257.Google Scholar
5. Fuchs, L., Abelian groups, Publ. House of the Hungar. Acad. Sci. Budapest (1958).Google Scholar
6. Fuchs, L., Infinite abelian groups, Vol. I (Academic Press, New York, 1970), and Vol. II (Academic Press, New York, 1973).Google Scholar
7. Göbel, R. and Vergohsen, R., Intersection of pure subgroups of valuated abelian groups, Archiv der Math. 39 (1982), 525–534.Google Scholar
8. Megibben, C., On subgroups of primary abelian groups, Publ. Math. Debrecen 12 (1965), 293–294.Google Scholar
9. Nunke, R. J., Uniquely elongating modules, Symposia Math. 13 (1974), 315–330.Google Scholar
10. Richman, F. and Walker, E. A., Valuated groups, J. Algebra 56 (1979), 145–167.Google Scholar
11. Sake, L., Struttura dei p-gruppi abeliani, Bologna (1980).Google Scholar