Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T17:19:35.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Smoothness of Quotients Associated With a Pair of Commuting Involutions

Published online by Cambridge University Press:  20 November 2018

Aloysius G. Helminck  and
Gerald W. Schwarz
Aloysius G. Helminck
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695-8205, U.S.A. e-mail: [email protected]
Gerald W. Schwarz
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA 02454-9110, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

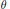Let $\sigma $, $\theta $ be commuting involutions of the connected semisimple algebraic group 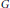$G$ where 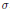$\sigma$, 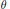$\theta $ and 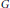$G$ are defined over an algebraically closed field 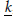$\underset{\scriptscriptstyle-}{k},$ char 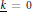$\underline{k}$=0. Let 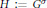$H:={{G}^{\sigma }}$ and 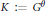$K:={{G}^{\theta }}$ be the fixed point groups. We have an action 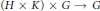$\left( H\,\times \,K \right)\,\times \,G\,\to \,G$, where 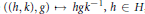$\left( \left( h,\,k \right),\,g \right)\,\mapsto \,hg{{k}^{-1}},\,h\,\in \,H$ , 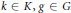$k\,\in \,K,g\,\in \,G$. Let $G\,//\,\left( H\,\times \,K \right)$ denote the categorical quotient Spec 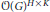$\mathcal{O}{{(G)}^{H\times K}}$ . We determine when this quotient is smooth. Our results are a generalization of those of Steinberg [Ste75], Pittie [Pit72] and Richardson [Ric82] in the symmetric case where 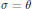$\sigma \,=\,\theta $ and $H\,=K$.

Keywords

20G1520G2022E46
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 5 , 01 October 2004 , pp. 945 - 962
Copyright
Copyright © Canadian Mathematical Society 2004

References

[BdS49] Borel, A. and de Siebenthal, J., Les sous-groupes fermés de rang maximum des groupes de Lie clos. Comment. Math. Helv. 23(1949), 200–221.Google Scholar
[Dyn52] Dynkin, E. B., Semisimple subalgebras of semisimple Lie algebras. Mat. Sbornik N.S. 30(72)(1952), 349–462.Google Scholar
[Helg84] Helgason, S., Groups and Geometric Analysis. Academic Press, Orlando, FL, 1984.Google Scholar
[Hel88] Helminck, A. G., Algebraic groups with a commuting pair of involutions and semisimple symmetric spaces. Adv. in Math. 71(1988), 21–91.Google Scholar
[HS01] Helminck, A. G. and Schwarz, G. W., Orbits and invariants associated with a pair of commuting involutions. Duke Math. J. 106(2001), 237–279.Google Scholar
[Mat80] Matsumura, H., Commutative Algebra. Benjamin/Cummings, Reading, MA, 1980.Google Scholar
[Pit72] Pittie, H. V., Homogeneous vector bundles on homogeneous spaces. Topology 11(1972), 192–203.Google Scholar
[Ric81] Richardson, R. W., An application of the Serre Conjecture to semisimple algebraic groups. Lecture Notes in Mathematics 848, Springer-Verlag, Berlin, 1981, pp. 141–152.Google Scholar
[Ric82] Richardson, R. W., Orbits, invariants and representations associated to involutions of reductive groups. Invent. Math. 66(1982), 287–312.Google Scholar
[Rui89] Ruitenburg, G., Invariant ideals of polynomial algebras and multiplicity free group action. Compositio Math. 71(1989), 181–227.Google Scholar
[Ste68] Steinberg, R., Endomorphisms of linear algebraic groups. Mem. Amer.Math. Soc., 80, Amer. Math. Soc., Providence, RI, 1968.Google Scholar
[Ste75] Steinberg, R., On a theorem of Pittie. Topology 14(1975), 173–177.Google Scholar
[Vus74] Vust, T., Opération de groupes réductifs dans un type de cônes presque homogènes. Bull. Soc. Math. France 102(1974), 317–334.Google Scholar