Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T03:27:36.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Formal Embeddings and the Residue Complex

Published online by Cambridge University Press:  20 November 2018

Amnon Yekutieli
Amnon Yekutieli*
Affiliation:
Department of Theoretical Mathematics, The Weizmann Institute of Science, Rehovot 76100, Israel
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 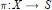$\pi :X\,\to \,S$ be a finite type morphism of noetherian schemes. A smooth formal embedding of 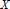$X$ (over $S$) is a bijective closed immersion 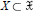$X\,\subset \,\mathfrak{X}$ , where 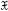$\mathfrak{X}$ is a noetherian formal scheme, formally smooth over $S$. An example of such an embedding is the formal completion 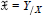$\mathfrak{X}={{Y}_{/X}}$ where 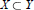$X\,\subset \,Y$ is an algebraic embedding. Smooth formal embeddings can be used to calculate algebraic De Rham(co)homology.

Our main application is an explicit construction of the Grothendieck residue complex when $S$ is a regular scheme. By definition the residue complex is the Cousin complex of 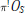${{\pi }^{!}}{{O}_{S}}$, as in 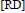$[\text{RD}]$. We start with 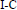$\text{I-C}$. Huang's theory of pseudofunctors on modules with 0-dimensional support, which provides a graded sheaf 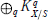${{\oplus }_{q}}K_{X/S}^{q}.$ We then use smooth formal embeddings to obtain the coboundary operator 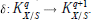$\delta :K_{X/S}^{q}\to K_{X/S}^{q+1}.$ We exhibit a canonical isomorphism between the complex 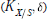$K_{X/S}^{\cdot },\delta $ and the residue complex of 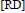$[\text{RD}]$. When $\pi $ is equidimensional of dimension $n$ and generically smooth we show that ${{\text{H}}^{-n}}K_{X/S}^{\cdot }$ is canonically isomorphic to to the sheaf of regular differentials of Kunz-Waldi 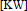$[\text{KW}]$.

Another issue we discuss is Grothendieck Duality on a noetherian formal scheme 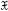$\mathfrak{X}$ . Our results on duality are used in the construction of 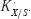$K_{X/S}^{\cdot }$.

Keywords

14B2014F1014B1514F20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 863 - 896
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

Incumbent of the Anna and Maurice Boukstein Career Development Chair.

References

[AJL1] Alonso, L., A. Jeremías and Lipman, J., Local homology and cohomology on schemes. Ann. Sci. Éc. Norm. Sup. 30(1997), 1–39.Google Scholar
[AJL2] Alonso, L., Grothendieck Duality on formal schemes. preprint (eprint: alg-geom/9708006).Google Scholar
[Bo] Borel, A. et al., Algebraic D-Modules. Academic Press, Boston, 1987.Google Scholar
[CA] Bourbaki, N., Commutative Algebra. Hermann, Paris, 1972.Google Scholar
[EGA] Grothendieck, A. and Dieudonné, J., Éléments de Géometrie Algébrique. [EGA] I: Springer-Verlag, Berlin, 1971.Google Scholar
[EGA] Grothendieck, A., II–IV: Inst. Hautes Études Sci. Publ. Math. 8, 11, 17, 20, 24, 28, 32.Google Scholar
[Gr] Grothendieck, A., On the De Rham cohomology of algebraic varieties. Inst. Hautes Études Sci. Publ.Math. 29(1966), 95–103.Google Scholar
[Ha] Hartshorne, R., On the De Rham Cohomology of algebraic varieties. Inst. Hautes Études Sci. Publ. Math. 45(1975), 5–99.Google Scholar
[Hg1] Huang, I-C., Pseudofunctors on Modules with Zero Dimensional Support. Mem. Amer. Math. Soc. 548(1995), Providence.Google Scholar
[Hg2] Huang, I-C., An explicit construction of residual complexes. preprint.Google Scholar
[Hg3] Huang, I-C., Residue theorem via an explicit construction of traces. preprint.Google Scholar
[HK1] Hübl, R. and Kunz, E., Integration of Differential Forms on Schemes. J. Reine Angew. Math. 410(1990), 53–83.Google Scholar
[HK2], Regular differential forms and duality for projective morphisms. J. Reine Angew. Math. 410(1990), 84–108.Google Scholar
[HS] Hübl, R. and Sastry, P., Regular differential forms and relative duality. Amer. J. Math. (4) 115(1993), 749–787.Google Scholar
[Hu] Hübl, R., Residues of regular and meromorphic differential forms. Math. Ann. 300(1994), 605–628.Google Scholar
[Ku] Kunz, E., Kähler Differentials. Vieweg, Braunschweig, Wiesbaden, 1986.Google Scholar
[KW] Kunz, E. and Waldi, R., Regular Differential Forms. Contemporary Math. 79(1988), Amer. Math. Soc., Providence.Google Scholar
[Li] Lipman, J., Dualizing sheaves, differentials and residues on algebraic varieties. Astérisque 117(1984).Google Scholar
[LS1] Lipman, J. and Sastry, P., Regular differentials and equidimensional scheme-maps. J. Algebra Geom. 1(1992), 101–130.Google Scholar
[LS2] Lipman, J., Residues and duality for Cousin complexes. preprint.Google Scholar
[Ma] Matsumura, H., Commutative Algebra. Benjamin/Cummings, Reading, Massachusetts, 1980.Google Scholar
[Mi] Milne, J. S., Étale Cohomology. Princeton Univ. Press, Princeton, New Jersey, 1980.Google Scholar
[RD] Hartshorne, R., Residues and Duality. Lecture Notes in Math. 20, Springer-Verlag, Berlin, 1966.Google Scholar
[Sa] Sastry, P., Residues and duality on algebraic schemes. Compositio Math. 101(1996), 133–178.Google Scholar
[SY] Sastry, P. and Yekutieli, A., On residue complexes, dualizing sheaves and local cohomology modules. Israel J. Math. 90(1995), 325–348.Google Scholar
[Ta] Tate, J., Genus change in extensions of function fields. Proc. Amer. Math. Soc. 3(1952), 400–406.Google Scholar
[Ye1] Yekutieli, A., An Explicit Construction of the Grothendieck Residue Complex (with an appendix by P. Sastry). Astérisque 208(1992).Google Scholar
[Ye2] Yekutieli, A., Traces and differential operators over Beilinson completion algebras. Compositio Math. 99(1995), 59–97.Google Scholar
[Ye3] Yekutieli, A., Residues and differential operators on schemes. Duke Math. J., to appear.Google Scholar
[Ye4], The action of adeles on the residue complex. preprint.Google Scholar