Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:26:04.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Boundary Values Along Totally Real Submanifolds

Published online by Cambridge University Press:  20 November 2018

Edgar Lee Stout
Edgar Lee Stout*
Affiliation:
University of Washington, Seattle, Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result of this paper is the following regularity result:

THEOREM. Let D ⊂ CNbe a bounded, strongly pseudoconvex domain with bD of class Ck, k ≧ 3. Let Σ ⊂ bD be an N-dimensional totally real submanifold, and let f ∊ A(D) satisfy |f| = 1 on Σ, |f| < 1 on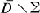. If Σ is of class Cr, 3 ≦ r < k, then the restriction fΣ = f|Σ of f to Σ is of class Cr − 0, and if Σ is of class Ck, then fΣ is of class Ck − 1.

Here, of course, A(D) denotes the usual space of functions continuous on 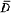, holomorphic on D, and we shall denote by Ak(D), k = 1, 2, …, the space of functions holomorphic on D whose derivatives or order k lie in A(D).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 2 , 01 April 1984 , pp. 240 - 248
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Burns, D. and Stout, E. L., Extending functions from submanifolds of the boundary, Duke Math. J. 43 (1976), 391–404.Google Scholar
2. Chirka, E. M., Regularanosf granic analiticheskikh mnozhestv, Mat. Sb. 117 (159) (1982), 291–336. English translation Math. USSR Sb. 45 (1983), 291–335.Google Scholar
3. Dieudonné, J., Foundations of modem analysis (Academic Press, New York and London, 1960).Google Scholar
4. Duchamp, T., The classification of Le gendre embeddings, Ann. Inst. Fourier (Grenoble), to appear.Google Scholar
5. Duchamp, T. and Stout, E. L., Maximum modulus sets, Ann. Inst. Fourier (Grenoble) 41 (1981), 37–69.Google Scholar
6. Hardy, G. H. and Littlewood, J. E., Some properties of fractional integrals, Math. Z. 34 (1932), 403–439. (Also in the Collected works of G. H. Hardy, vol. III, 627–664, Oxford Univ. Press, Oxford, 1969.)Google Scholar
7. Hill, C. D. and Taiani, G., Families of analytic discs with boundaries on a prescribed CR submanifold, Ann. Scuola Norm. Sup. Pisa, CI. Sci. 5 (1978), 327–380.Google Scholar
8. Nagel, A. and Wainger, S., Limits of bounded holomorphic functions along curves, pp. 327–344 in Recent developments in several complex variables, Ann. Math. Studies 100 (Princeton Univ. Press, Princeton, 1981).Google Scholar
9. Narasimhan, R., Analysis on real and complex manifolds (Masson et Cie., Paris, and North Holland Publishing Co., Amsterdam, 1973).Google Scholar
10. Pinchuk, S. I., A boundary uniqueness theorem for holomorphic functions of several complex variables, Math. Notes 15 (1974), 116–120.Google Scholar
11. Priwalow, I. I., Randeigenschaften Analytischer Funktionen (VEB Deutscher Verlag der Wissenschaften, Berlin, 1956).Google Scholar
12. Rudin, W., Function theory in the unit ball of Cn (Springer-Verlag, Berlin, Heidelberg, New York, 1981).Google Scholar
13. Rudin, W., Peak interpolation manifolds of class C1 , Pacific J. Math. 75 (1978), 267–279.Google Scholar
14. Stout, E. L., Interpolation manifolds, pp. 373–391 in Recent developments in several complex variables, Ann. Math. Studies 100 (Princeton University Press, Princeton, 1981).Google Scholar
15. Tsuji, M., Potential theory in modern function theory (Maruzen, Tokyo, 1959).Google Scholar