Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T06:22:01.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Small Prime Solutions of Quadratic Equations

Published online by Cambridge University Press:  20 November 2018

Kwok-Kwong Stephen Choi  and
Jianya Liu
Kwok-Kwong Stephen Choi
Affiliation:
Department of Mathematics Simon Fraser University Burnaby, BC V5A 1S6, email: [email protected]
Jianya Liu
Affiliation:
Department of Mathematics Shandong University Jinan, Shandong 250100 P. R. China, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 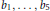${{b}_{1}},...,{{b}_{5}}$ be non-zero integers and $n$ any integer. Suppose that 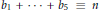${{b}_{1}}+\cdot \cdot \cdot +{{b}_{5}}\equiv n$ (mod 24) and 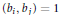$\left( {{b}_{i}},{{b}_{j}} \right)=1$ for 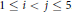$1\le i<j\le 5$. In this paper we prove that

  1. (i) if all 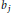${{b}_{j}}$ are positive and 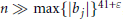$n\gg \max {{\left\{ \left| {{b}_{j}} \right| \right\}}^{41+\varepsilon }}$, then the quadratic equation 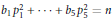${{b}_{1}}p_{1}^{2}+\cdot \cdot \cdot +{{b}_{5}}p_{5}^{2}=n$ is soluble in primes 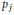${{p}_{j}}$, and

  2. (ii) if 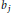${{b}_{j}}$ are not all of the same sign, then the above quadratic equation has prime solutions satisfying 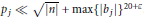${{p}_{j}}\ll \sqrt{\left| n \right|}+\max {{\left\{ \left| {{b}_{j}} \right| \right\}}^{20+\varepsilon }}$.

Keywords

11P3211P0511P55
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 1 , 01 February 2002 , pp. 71 - 91
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Baker, A., On some diophantine inequalities involving primes. J. Reine Angew. Math. 228 (1967), 166–181.Google Scholar
[2] Bauer, C., Liu, M. C. and Zhan, T., On sums of three prime squares. J. Number Theory 85 (2000), 336–359.Google Scholar
[3] Choi, K. K., A numerical bound for Baker's constant—some explicit estimates for small prime solutions of linear equations. Bull. Hong Kong Math. Soc. 1 (1997), 1–19.Google Scholar
[4] Davenport, H., Multiplicative Number Theory. 2nd edition, Springer, Berlin, 1980.Google Scholar
[5] Gallagher, P. X., A large sieve density estimate near σ = 1. Invent. Math. 11 (1970), 329–339.Google Scholar
[6] Heath-Brown, D. R., Prime numbers in short intervals and a generalized Vaughan's identity. Canad. J. Math. 34 (1982), 1365–1377.Google Scholar
[7] Hua, L. K., Some results in the additive prime number theory. Quart. J. Math. (Oxford) 9 (1938), 68–80.Google Scholar
[8] Hua, L. K., Additive theory of prime numbers (in Chinese). Science Press, Beijing 1957; English transl., Amer. Math. Soc., Rhode Island, 1965.Google Scholar
[9] Huxley, M. N., Large values of Dirichlet polynomials (III). Acta Arith. 26(1974/75), 435–444.Google Scholar
[10] Liu, J. Y. and Liu, M. C., The exceptional set in the four prime squares problem. Illinois J. Math. 44 (2000), 272–293.Google Scholar
[11] Liu, J. Y., Liu, M. C. and Zhan, T., Squares of primes and powers of 2. Monatsh. Math. 128 (1999), 283–313.Google Scholar
[12] Liu, M. C., and Tsang, K. M., Small prime solutions of linear equations. In: Théorie des nombres (eds. J.-M. De Koninck and C. Levesque), Walter de Gruyter, Berlin-New York, 1989, 595–624.Google Scholar
[13] Liu, M. C., and Tsang, K. M., Small prime solutions of some additive equations. Monatsh. Math. 111 (1991), 147–169.Google Scholar
[14] Liu, M. C., and Wang, T. Z., A numerical bound for small prime solutions of some ternary linear equations. Acta Arith. 86 (1998), 343–383.Google Scholar
[15] Prachar, K., Primzahlverteilung. Springer, Berlin, 1957.Google Scholar
[16] Titchmarsh, E. C., The theory of the Riemann zeta-function. 2nd edition, Oxford University Press, Oxford, 1986.Google Scholar