Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T23:54:18.483Z Has data issue: false hasContentIssue false
  • English
  • Français

Six Primes and an Almost Prime in Four Linear Equations

Published online by Cambridge University Press:  20 November 2018

Antal Balog
Antal Balog*
Affiliation:
Mathematical Institute Mathematics Department Budapest 1364, P. O. Box 127 Hungary, e-mail: [email protected] Mathematics Department University of Michigan Ann Arbor, Michigan 48109-1003 U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are infinitely many triplets of primes 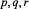$p,\,q,\,r$ such that the arithmetic means of any two of them, 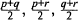$\frac{p+q}{2},\,\frac{p+r}{2},\,\frac{q+r}{2}$ are also primes. We give an asymptotic formula for the number of such triplets up to a limit. The more involved problem of asking that in addition to the above the arithmetic mean of all three of them, 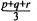$\frac{p+q+r}{3}$ is also prime seems to be out of reach. We show by combining the Hardy-Littlewood method with the sieve method that there are quite a few triplets for which six of the seven entries are primes and the last is almost prime.

Keywords

11P3211N36
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 465 - 486
Copyright
Copyright © Canadian Mathematical Society 1998

References

[B 1990] Balog, A., The prime k-tuplets conjecture on average. Analytic Number Theory, (eds. Brendt, B., Diamond, H.G., Halberstam, H. and Hildebrand, A.), Birkhauser, 1990. 47-75.Google Scholar
[B 1992] Balog, A., Linear equations in primes. Mathematika 39(1992), 367-378.Google Scholar
[B,B 1995] Balog, A. and Briidem, J., Sums of three cubes in three linked three-progressions. J. Reine Angew. Math. 466(1995), 45-85.Google Scholar
[C 1973] Chen, J.-R., On the representation of a large even integer as the sum of a prime and a product of at most two primes. Sci. Smica 16(1973), 157—176.Google Scholar
[H,R 1974] Halberstam, H. and Richert, H.E., Sieve methods. Academic Press, London, 1974.Google Scholar
[H-B 1981] D. Heath-Brown, R., Three primes and an almost-prime in arithmetic progression. J. London Math. Soc. (2) 23(1981), 396-414.Google Scholar
[11972] Iwaniec, H., Primes of the type ϕ(x,y)+A, where is a quadratic form. Acta Arith. 21(1972), 203-234.Google Scholar
[L 1961] Lavrik, A.F., On the theory of distribution of primes based on I. M. Vinogradov's method of trigonometric sums. Trudy Mat. Inst. Steklov 64(1961), 90-125.Google Scholar
[vdC 1939] J. van der Corput, G., Uber Summen von Primzahlen und Primzahlquadraten. Math. Ann. 116 (1939), 1–50.Google Scholar