Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T14:01:23.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular Integrals on Product Spaces Related to the Carleson Operator

Published online by Cambridge University Press:  20 November 2018

Elena Prestini
Elena Prestini*
Affiliation:
Departimento di Matematica, Seconda Università di Roma, 00133 Rome, Italy e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove 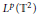${{L}^{p}}({{\mathbb{T}}^{2}})$ boundedness, 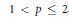$1\,<\,p\,\le \,2$, of variable coefficients singular integrals that generalize the double Hilbert transform and present two phases that may be of very rough nature. These operators are involved in problems of a.e. convergence of double Fourier series, likely in the role played by the Hilbert transform in the proofs of a.e. convergence of one dimensional Fourier series. The proof due to C.Fefferman provides a basis for our method.

Keywords

42B2042B08
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 1 , 01 February 2006 , pp. 154 - 179
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Carleson, L., On convergence and growth of partial sumas of Fourier series. Acta Math. 116(1966), 135–157.Google Scholar
[2] Fefferman, C., The multiplier problem for the ball. Ann. of Math. 94(1971), 330–336.Google Scholar
[3] Fefferman, C., On the divergence of multiple Fourier series. Bull. of Amer.Math. Soc. 77(1971), 191–195.Google Scholar
[4] Fefferman, C., On the convergence of multiple Fourier series. Bull. Amer. Math. Soc. 77(1971), 744–745.Google Scholar
[5] Fefferman, C., Pointwise convergence of Fourier series. Ann. of Math. 98(1973), 551–572.Google Scholar
[6] Fefferman, C., Erratum: Pointwise convergence of Fourier series. Ann. of Math. 146(1997), 239.Google Scholar
[7] Fefferman, R., Singular integrals on product domains. Bull. Amer. Math. Soc. 4(1981), no. 2, 195–201.Google Scholar
[8] Fefferman, R. and Stein, E. M., Singular integrals on product spaces. Adv. in Math. 45(1982), no. 2, 117–143.Google Scholar
[9] Garcia-Cuerva, J. and Rubio de Francia, J. L., Weighted Norm Inequalities and Related Topics. North-Holland, Amsterdam, 1985.Google Scholar
[10] Gosselin, J. A., On the convergence of Walsh-Fourier series for L 2(0, 1). In: Studies in Analysis, Adv. Math. Suppl. Stud. 4, Academic Press, New York, 1979, pp. 223–231.Google Scholar
[11] Harris, D. C., Almost everywhere divergence of multiple Walsh-Fourier series. Proc. Amer. Math. Soc. 101(1987), no. 4, 637–643.Google Scholar
[12] Hunt, R. A., On the convergence of Fourier series. In: Orthogonal Expansions and their Continuous Analogues, Southern Illinois University Press, Carbondale, IL, 1968, pp. 235–255.Google Scholar
[13] Hunt, R. A., Almost everywhere convergence of Walsh-Fourier series of L 2 functions. In: Actes du Congrès International des Mathématiciens, vol. 2, Gauthier-Villars, Paris, 1970, pp. 655–661.Google Scholar
[14] Hunt, R. A. and Young, W. S., A weighted norm inequality for Fourier series. Bull. Amer. Math. Soc. 80(1974), 274–277.Google Scholar
[15] Journé, J. L., Calderón-Zygmund operators on product spaces. Rev. Mat. Iberoamericana 3(1985), 55–92.Google Scholar
[16] Prestini, E., On the two proofs of pointwise convergence of Fourier series. Amer. J. Math. 104(1982), no. 1, 127–139.Google Scholar
[17] Prestini, E., Variants of the maximal double Hilbert transform. Trans. Amer. Math. Soc. 290(1985), no. 2, 761–771.Google Scholar
[18] Prestini, E., Uniform estimates for families of singular integrals and double Fourier series. J. Austral. Math. Soc. Ser. A 41(1986), no. 1, 1–12.Google Scholar
[19] Prestini, E., L 2 boundedness of highly oscillatory integrals on product domains. Proc. Amer. Math. Soc. 104(1988), no. 2, 493–497.Google Scholar
[20] Prestini, E., Singular integrals with highly oscillating kernels on product spaces. Colloq. Math. 86(2000), no. 1, 9–13.Google Scholar
[21] Prestini, E., Singular integrals with bilinear phases. Acta Math. Sinica, to appear.Google Scholar
[22] Prestini, E. and Sjölin, P., A Littlewood-Paley inequality for the Carleson operator. J. Fourier Anal. Appl. 6(2000), no. 5, 457–466.Google Scholar
[23] Stein, E. M., Singular Integrals and Differentiability Properties of Functions. Princeton Mathematical Series 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar