Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T14:11:39.369Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous Polynomial Approximations of the Lerch Function

Published online by Cambridge University Press:  20 November 2018

Tanguy Rivoal
Tanguy Rivoal*
Affiliation:
Institut Fourier, CNRS UMR 5582, Université Grenoble 1, 100 rue des Maths, BP 74, 38402 Saint-Martin d’Hères cedex, France. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct bivariate polynomial approximations of the Lerch function that for certain specialisations of the variables and parameters turn out to be Hermite–Padé approximants either of the polylogarithms or of Hurwitz zeta functions. In the former case, we recover known results, while in the latter the results are new and generalise some recent works of Beukers and Prévost. Finally, we make a detailed comparison of our work with Beukers’. Such constructions are useful in the arithmetical study of the values of the Riemann zeta function at integer points and of the Kubota–Leopold 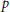$p$ -adic zeta function.

Keywords

41A1041A2111J72
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1341 - 1356
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Andrews, G. E., Askey, R. A., and Roy, R., Special Functions. Encyclopedia of Mathematics and Its Applications 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[2] Apéry, R., Irrationalité de ζ(2) et ζ(3), Astérisque 61(1979), 11–13.Google Scholar
[3] Baker, G. A. and Graves-Morris, P., Padé Approximants. Second edition. Encyclopedia of Mathematics and its Applications 59, Cambridge University Press, Cambridge, 1996.Google Scholar
[4] Ball, K. and Rivoal, T., Irrationalité d’une infinité de valeurs de la fonction zêta aux entiers impairs. Invent. Math. 146(2001), no. 1, 193–207.Google Scholar
[5] Beukers, F., Padé-approximations in number theory. In: Padé Approximation and Its Applications, Lecture Notes in Math. 888, Springer, Berlin, 1981, pp. 90–99.Google Scholar
[6] Beukers, F., Irrationality proofs using modular forms, Journées arithmétiques de Besanҫon. Astérisque No. 147-148(1987), 271–283, 345.Google Scholar
[7] Beukers, F., Irrationality of some p-adic L-values. Acta math. Sin. 24(2008), no. 4, 663–686.Google Scholar
[8] Calegari, F., Irrationality of certain p-adic periods for small p. Int. Math. Res. Not. 2005, no. 20, 1235–1249.Google Scholar
[9] Chudnovsky, G. V., Padé approximations to the generalized hypergeometric functions. I. J. Math. Pures Appl. 58(1979), no. 4, 445–476.Google Scholar
[10] Fischler, S. and Rivoal, T., Approximants de Padé et séries hypergéométriqueséquilibrées. J. Math. Pures Appl. 82(2003), no. 10, 1369–1394.Google Scholar
[11] Nikišin, E. M., Irrationality of values of functions F(x, s). Mat. Sb. 109(151)(1979), no. 3, 410–417, 479.Google Scholar
[12] Nikišin, E. M. and Sorokin, V. N., Rational Approximations and Orthogonality. Translations of Mathematical Monographs 92, American Mathematical Society, Providence, RI, 1991.Google Scholar
[13] Nörlund, N.-E., Leҫons sur les séries d’interpolation, Collection de monographies sur la théorie des fonctions, Gauthier-Villars, 1926.Google Scholar
[14] Prévost, M., A new proof of the irrationality of ζ(2) and ζ(3) using Padé approximants. J. Comput. Appl. Math. 67(1996), no. 2, 219–235.Google Scholar
[15] Rivoal, T., La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs. C. R. Acad. Sci. Paris Sér. I Math. 331(2000), no. 4, 267–270.Google Scholar
[16] Rivoal, T., Indépendance linéaire de valeurs des polylogarithmes, J. Théor. Nombres Bordeaux 15(2003), no. 2, 551–559.Google Scholar
[17] Rivoal, T., Nombres d’Euler, approximants de Padé et constante de Catalan, Ramanujan J. 11(2006), no. 2, 199–214.Google Scholar
[18] Rivoal, T., Applications arithmétiques de l’interpolation lagrangienne. Int. J. Number Theory 5(2009), 1–24.Google Scholar
[19] Slater, L. J., Generalized Hypergeometric Functions. Cambridge University Press, Cambridge, 1966.Google Scholar
[20] Wilson, J. A., Some hypergeometric orthogonal polynomials. SIA MJ. Math. Anal. 11(1980), no. 4, 690–701.Google Scholar